-
23.(14分)已知倾斜角为
 的直线
的直线 过点
过点 和点
和点 ,其中
,其中 在第一象限,且
在第一象限,且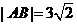
(Ⅰ)求点
 的坐标;
的坐标;(Ⅱ)若直线
 与双曲线
与双曲线
 相交于不同的两点
相交于不同的两点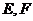 ,且线段
,且线段 的中点坐标为
的中点坐标为 ,求实数
,求实数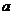 的值。
的值。 -
23. 解:(Ⅰ) 直线
 方程为
方程为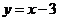 ,设点
,设点 ,
,
由

及
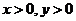 ,得
,得 ,
,∴点
 的坐标为
的坐标为
(Ⅱ)由
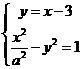 得
得 ,
, 设
 ,则
,则 ,得
,得 ,
, 此时,
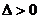 ,∴
,∴ 。
。
-
22.(本小题满分14分)已知椭圆C的方程为
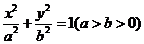 ,双曲线
,双曲线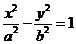 的两条渐近线为
的两条渐近线为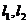 ,过椭圆C的右焦点F的直线
,过椭圆C的右焦点F的直线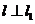 ,又
,又 与
与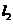 交于P点,设
交于P点,设 与椭圆C的两个交点由上至下依次为A,B.
与椭圆C的两个交点由上至下依次为A,B.(1) 当
 与
与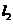 夹角为
夹角为 且
且 时,求椭圆C的方程.
时,求椭圆C的方程.(2) 求
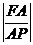 的最大值.
的最大值. -
22.

 解:(1)
解:(1)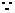
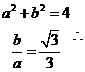
 故
故 (6分)
(6分)(2)
 联立
联立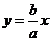 得
得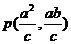 (8分)
(8分)设A分
 的比为
的比为 ,则A
,则A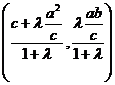
代入
 ,整理化简得:
,整理化简得: (12分)
(12分)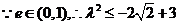 即
即 的最大值为
的最大值为
(18)本小题满分14分
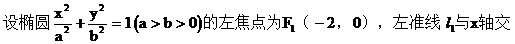




圆中,求面积最小的圆的半径长。
(18)解:
 ………………1分
………………1分
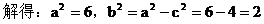 ………………3分
………………3分 ………………4分
………………4分

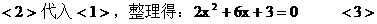 …………6分
…………6分
 ………………7分
………………7分

 ………………11分
………………11分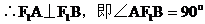
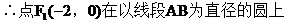 ………………12分
………………12分(III)面积最小的圆的半径应是点F到直线l的距离,设为r………………13分
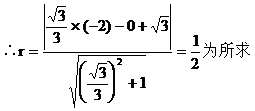 ………………14分
………………14分

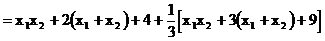

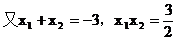
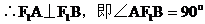

-
22. 已知ΔOFQ的面积为2,且.=m .
(1)设<m<4,求向量与的夹角θ正切值的取值范围;
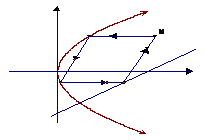
 (2)设以O为中心,F为焦点的双曲线经过点Q(如图),||=c,m=(-1)c2,当||取得最小值时,求此双曲线的方程.(本题满分14分)
(2)设以O为中心,F为焦点的双曲线经过点Q(如图),||=c,m=(-1)c2,当||取得最小值时,求此双曲线的方程.(本题满分14分) -
22.(1)∵,∴tanθ=.
又∵<m<4,∴1<m<4.………………………………6分
(2)设所求的双曲线方程为(a>0,b>0),Q(x1,y1),
则=(x1-c,y1),∴S△OFQ= ||.|y1|=2,∴y1=±.
又由.=(c,0).(x1-c,y1)=(x1-c)c=(-1)c2,∴x1=c.…………8分
∴||==≥.
当且仅当c=4时, ||最小,这时Q点的坐标为(,)或(,-).……12分
∴, ∴.
故所求的双曲双曲线方程为
-
20.
 抛物线有光学性质,即由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出,如右图所示,今有抛物线
抛物线有光学性质,即由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出,如右图所示,今有抛物线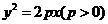 ,一光源在点
,一光源在点 处,由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P,反射后,又射向抛物线上的点Q,再反射后又沿平行于抛物线的轴的方向射出,途中遇到直线
处,由其发出的光线沿平行于抛物线的轴的方向射向抛物线上的点P,反射后,又射向抛物线上的点Q,再反射后又沿平行于抛物线的轴的方向射出,途中遇到直线 上的点N,再反射后又射回点M。
上的点N,再反射后又射回点M。(1)设P、Q两点的坐标分别是
 ,
,证明:
 。
。(2)求抛物线方程。(14分)
-
20.解(1)由抛物线的光学性质及题意知光线PQ必过抛物线的焦点
 ,设
,设 ,代入抛物线方程得:
,代入抛物线方程得: ,
, (6分)
(6分)(2)设
 ,由题意知
,由题意知 ,又设
,又设 是点M关于直线l的对称点,则有:
是点M关于直线l的对称点,则有: ,
, ,
,由对称性质知
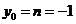 ,代入直线l的方程得
,代入直线l的方程得 (或利用到角公式得
(或利用到角公式得 ,求出
,求出 )。由
)。由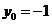 ,则
,则 ,又P,F,Q三点共线得P=2。抛物线方程为
,又P,F,Q三点共线得P=2。抛物线方程为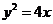 。(14分)
。(14分)