-
1.过点
 作圆
作圆 的切线
的切线 已知直线
已知直线 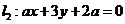 与
与 平行,则
平行,则 与
与 之间的距离为(
)
之间的距离为(
)(A)
 (B)
(B) (C)
(C) (D)
(D)
-
2.已知两直线
 和
和 当
当 时,
时,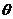 =__________________;当
=__________________;当 时,
时,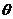 =____________________.
=____________________. -
3.已知双曲线的一条准线与渐近线的交点为A、B,这条准线的相应焦点为F,如果
 是等边三角形,那么此双曲线的离心率为________.
是等边三角形,那么此双曲线的离心率为________.二:圆锥曲线的定义与方程
1:椭圆的第一定义
 ;
; 2:双曲线的第一定义
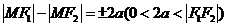 ;
;3:统一定义
 (
(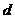 为动点
为动点 到相应准线的距离)
到相应准线的距离)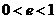 时为椭圆:
时为椭圆: 时为双曲线:
时为双曲线: 时为抛物线。
时为抛物线。[例3]
 是椭圆
是椭圆 上一点,
上一点, 、
、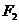 是焦点,若
是焦点,若 则
则 的面积是_______________.
的面积是_______________.[例4]过双曲线
 的右焦点
的右焦点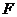 作一条长为
作一条长为 的弦
的弦 (A、B均在双曲线的的右支上),将双曲线绕右准线旋转
(A、B均在双曲线的的右支上),将双曲线绕右准线旋转 ,则弦
,则弦 扫过的面积为(
)
扫过的面积为(
)(A)
 (B)
(B) (C)
(C) (D)
(D)
[例5]已知点
 为抛物线
为抛物线 上任一点,
上任一点, 到
到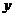 轴上的距离为
轴上的距离为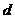 ,则
,则 +
+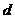 的最小值为_____________.
的最小值为_____________.加强练习:
-
4.
 是长轴在
是长轴在 轴上的椭圆
轴上的椭圆 上的点,
上的点, 、
、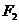 分别为椭圆的两个焦点,椭圆的半焦距为
分别为椭圆的两个焦点,椭圆的半焦距为 ,则
,则 的最大值与最小值之差一定是(
)
的最大值与最小值之差一定是(
)(A)1 (B)
 (C)
(C) (D)
(D)
-
5.抛物线
 与椭圆
与椭圆 在
在 轴上方的交点为A、B,设
轴上方的交点为A、B,设 的左顶点为F,则
的左顶点为F,则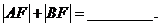
-
6.设
 、
、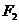 是双曲线
是双曲线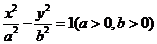 的两个焦点,P是双曲线上一点,且
的两个焦点,P是双曲线上一点,且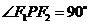 ,已知双曲线的离心率为
,已知双曲线的离心率为 ,
, 的面积是9,则
的面积是9,则 =(
)
=(
)(A)4 (B)5 (C)6 (D)7
三:直线与圆锥曲线 联立直线与圆锥曲线的方程,再结合函数与方程的思想来解决问题。
[例6]直线
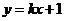 与双曲线
与双曲线 的左支交于A、B两点,直线
的左支交于A、B两点,直线 过点
过点 和
和 的中点
的中点 ,求直线
,求直线 在
在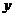 轴上的截距
轴上的截距 的取值范围。
的取值范围。四:轨迹问题 解题步骤:建标设点、列式、化简、讨论。注意结合定义和利用平面几何知识解题。
[例7]以
 为圆心的圆与椭圆
为圆心的圆与椭圆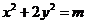 交于A、B两点,求
交于A、B两点,求 中点
中点 的轨迹方程。
的轨迹方程。[例8]已知圆
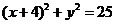 的圆心为
的圆心为 ,圆
,圆 的圆心为
的圆心为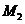 ,一动圆
,一动圆 与这两个圆都外切。求动圆圆心
与这两个圆都外切。求动圆圆心 的轨迹。
的轨迹。综合练习
-
1.“抛物线
 上离点
上离点 最近的点恰好为顶点。”成立的充要条件是(
)
最近的点恰好为顶点。”成立的充要条件是(
)(A)
 (B)
(B) (C)
(C) (D)
(D)
-
2.设双曲线
 的半焦距
的半焦距 ,直线
,直线 过
过 两点,已知原点到
两点,已知原点到 的距离为
的距离为 ,则双曲线的离心率为(
)
,则双曲线的离心率为(
)(A)2 (B)
 (C)
(C)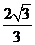 (D)
(D)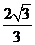 或2
或2 -
3.以椭圆
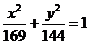 的右焦点为圆心,且与双曲线
的右焦点为圆心,且与双曲线 的两条渐近线都相切的圆的方程为____________________________.
的两条渐近线都相切的圆的方程为____________________________. -
4.已知点
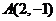 ,
, 为坐标原点,点
为坐标原点,点 在椭圆
在椭圆 上,则
上,则 +
+ 的最小值为__________________.
的最小值为__________________. -
5.
 无论实数
无论实数 取何值,直线
取何值,直线 与双曲线
与双曲线 总有公共点,则实数
总有公共点,则实数 的取值范围是_________________________.
的取值范围是_________________________. -
6.如图,已知椭圆中心O是坐标原点,F是
它的左焦点,A是它的左顶点,
 、
、 分别为
分别为左、右准线,
 交
交 轴于点B,
轴于点B, 、
、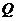 两点在
两点在椭圆上,且
 于M,
于M,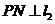 于N,
于N, ,下列5个比值中:①
,下列5个比值中:① ,
,②
 ,③
,③ ,④
,④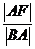 ,⑤
,⑤ ,其中等于该椭圆离心率的编号有___________.
,其中等于该椭圆离心率的编号有___________. -
7.抛物线
 的通径(即过焦点且垂直于对称轴的弦)为AB,
的通径(即过焦点且垂直于对称轴的弦)为AB, 是抛物线上异于
是抛物线上异于 、
、 的一个动点,分别过
的一个动点,分别过 、
、 作
作 、
、 的垂线
的垂线 、
、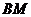 相交于
相交于 ,求点
,求点 的轨迹方程。
的轨迹方程。
专题 解析几何高考题型 一:考察解析几何中的基本量 如直线方程、点到直线的距离、圆及圆锥曲线的各种基本量。 [例1] 对于每个自然数,抛物线与轴交于、两点,以表示该两点间的距离,则的值是( ) (A) (B) (C) (D) [例2] (97年高考题)已知圆满足:①截轴所得弦长为2;②被轴分成两段圆弧,其弧长之比为3∶1;③圆心到直线的距离为,求该圆的方程。 加强练习:参考答案
答案
1、D 2、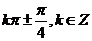 ;
;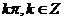 3、
3、 4、D 5、
4、D 5、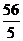 6、D
6、D
1、C 2、A
3、 4、5 5、
4、5 5、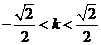
6、③④⑤ 7、