高考数学统一考试
理科数学
第Ⅱ卷(共90分)
-
(13)设O是坐标原点,F是抛物线y2=2px(p>0)的焦点,A是抛物线上的一点,
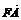 与x轴正向的夹角为60°,则
与x轴正向的夹角为60°,则 为
.
为
.(14)设D是不等式组
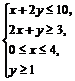 表示的平面区域,则D中的点P(x,y)到直线x+y=10距离的最大值是 .
表示的平面区域,则D中的点P(x,y)到直线x+y=10距离的最大值是 .(15)与直线x+y-2=0和曲线x2+y2-12x-12y+64=0都相切的半径最小的圆的标准方程是 .
(16)函数y=loga(x+3)-1(a>0,a
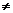 1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中mn>0,则
1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中mn>0,则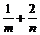 的最小值为
.
的最小值为
. -
(17)(本小题满分12分)
设数列
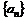 满足a1+2a1+32a1+…+3n-1an=
满足a1+2a1+32a1+…+3n-1an= .
.(Ⅰ)求数列
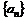 的通项;
的通项;(Ⅱ)设bn=
 ,求数列
,求数列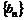 的前n项和Sn.
的前n项和Sn.(20)(本小题满分12分)
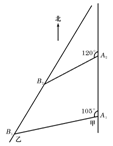 如图,甲船以每小时30
如图,甲船以每小时30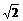 海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A1处时,乙船航行到甲船的北偏西120°方向的B1处,此时两船相距10
海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A1处时,乙船航行到甲船的北偏西120°方向的B1处,此时两船相距10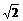 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?(21)(本小题满分12分)
已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C上的点到焦点距离的最大值为3;最小值为1;
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l1y=kx+m与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点.求证:直线l过定点,并求出该定点的坐标.
]
(22)(本小题满分14分)
设函数f(x)=x2+b ln(x+1),其中b≠0.
(Ⅰ)当b>
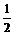 时,判断函数f(x)在定义域上的单调性;
时,判断函数f(x)在定义域上的单调性;(Ⅱ)求函数f(x)的极值点;
(Ⅲ)证明对任意的正整数n,不等式ln(
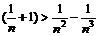 )都成立.
)都成立.