-
考试要求:1、掌握分类计数原理与分步计数原理,并能用它们分析和解决一些简单的应用问题。2、理解排列的意义,掌握排列数计算公式,并能用它解决一些简单的应用问题。
3、理解组合的意义,掌握组合数计算公式和组合数的性质,并能用它们解决一些简单的应用问题。4、掌握二项式定理和二项展开式的性质,并能用它们计算和证明一些简单的问题。
-
1、高三年级有文科、理科共9个备课组,每个人备课组的人数不少于4人,现从这9个备课组中抽出12人,每个备课组至少1人,组成“年级核心组”商议年级的有关事宜,则不同的抽调方案共有:
A.129种 B.148种 C.165种 D.585种
-
2、从4名教师与5名学生中任选3人,其中至少要有教师与学生各1人,则不同的选法共有:
A.140种 B.80种 C.70种 D.35种
-
3、 对某种产品的5件不同正品和4件不同次品一一进行检测,直到区分出所有次品为止. 若所有次品恰好经过五次检测被全部发现,则这样的检测方法有:
A.20种 B.96种 C.480种 D.600种
-
4、以长方体的8个顶点中的任意3个为顶点的三角形中,锐角三角形的个数是:
A.0 B.6 C.8 D.24
-
5、
 4个男生2个女生排成一排,若女生不能排在两端,且又不相邻,则不同的排法数有____________种。
4个男生2个女生排成一排,若女生不能排在两端,且又不相邻,则不同的排法数有____________种。 -
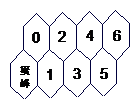
6、假定有一排蜂房,形状如图,一只蜜蜂在左下角,由于受了点
伤,只能爬,不能飞,而且只能永远向右方(包括右上,右下)
爬行,从一间蜂房爬到与之相邻的右蜂房中去,从最初位置爬
到6号蜂房共有 种不同的爬法。
-
7、某单位有六个科室,现从人才市场招聘来4名新毕业的大学生,要随机地安排到其中的两个科室且每科室2名,则不同的安排
 方案种数为
方案种数为A.
 B.
B.  C.
C.
 D.
D.
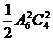
-
8、中央电视台“正大综艺”节目的现场观众来自四个单位,分别在图中的
四个区域内坐定.有四种不同颜色的服装,且相邻两个区域的颜色不同,
不相邻区域的观众服装颜色相同与否,不受限制,那么不同的着装方法
有:
A.36种 B.84种 C.48种 D.24种
-
9、6名运动员站在6条跑道上准备参加比赛,其中甲不能站在第一道也不能站在第二道,乙必须站在第五道或第六道,则不同排法种数共有
A. 144 B. 96 C. 72 D. 48
-
10、直线
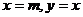 将圆面
将圆面 分成若干块. 现在用5种不同的颜色给这若干块涂色,每块只涂一种颜色,且任意两块不同色,若共有120种不同的涂法,则实数m的取值范围是
.
分成若干块. 现在用5种不同的颜色给这若干块涂色,每块只涂一种颜色,且任意两块不同色,若共有120种不同的涂法,则实数m的取值范围是
. -
11、用1个1,2个2,3个3这样6个数字可以组成多少个不同的6位数:
A.20 B.60 C.120 D.90
-
12、从-3,-2,-1,1,2,3中任取三个不同的数作为椭圆方程
 中的系数,则确定不同椭圆的个数为
.
中的系数,则确定不同椭圆的个数为
. -
13、 在
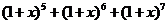 的展开式中,含
的展开式中,含 项的系数是首项为-2公差为3的等差数列的:
A.第13项 B.第18项 C.第11项
D.第20项
项的系数是首项为-2公差为3的等差数列的:
A.第13项 B.第18项 C.第11项
D.第20项 -
14、在
 的展开式中,
的展开式中, 项的系数是
项的系数是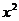 的系数与
的系数与 项系数的等比中项,则
项系数的等比中项,则 的值是:
A.
的值是:
A.  B.
B.  C.
C.
 D.
D.  15、若
15、若 的展开式中含有常数项(非零),则正整数n的可能值是:
的展开式中含有常数项(非零),则正整数n的可能值是:A.3 B.4 C.5 D.6
-
16、
 的展开式中
的展开式中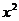 的系数是 ,如果展开式中第
的系数是 ,如果展开式中第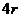 项和第
项和第 项的二项式系数相等,则
项的二项式系数相等,则 等于 .
等于 . -
17、已知二项式
 展开式的第4项与第5项之和为零,那么
展开式的第4项与第5项之和为零,那么 等于:
等于:A.1 B.
 C.2
D.46
C.2
D.46 -
18、若
 与
与 的展开式中各项系数之和分别为
的展开式中各项系数之和分别为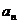 ,
,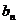 ,则
,则 =
.
=
. -
19、二项式(1+x)
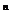 的展开式中, 存在着系数之比为5: 7的相邻两项, 则指数n (n
的展开式中, 存在着系数之比为5: 7的相邻两项, 则指数n (n N*)的最小值为:
N*)的最小值为: A. 13 B. 12 C. 11 D. 10
高考数学招生适应性考试试卷1参考答案
十、排列、组合、二项式定理参考答案
1、C;2、C;3、C;4、C;5、144;6、21;7、D;8、B;9、A;10、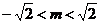 ;
;
11、B;12、36;13、D;14、B;15、C;16、-10,2;17、C;18、 ;19、C
;19、C