-
1.指数函数
(1)通过具体实例(如细胞的分裂,考古中所用的14C的衰减,药物在人体内残留量的变化等),了解指数函数模型的实际背景;
(2)理解有理指数幂的含义,通过具体实例了解实数指数幂的意义,掌握幂的运算。
(3)理解指数函数的概念和意义,能借助计算器或计算机画出具体指数函数的图象,探索并理解指数函数的单调性与特殊点;
(4)在解决简单实际问题的过程中,体会指数函数是一类重要的函数模型。
-
3.知道指数函数
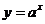 与对数函数
与对数函数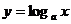 互为反函数(a>0,a≠1)。
互为反函数(a>0,a≠1)。 -
指数函数、对数函数、幂函数是三类常见的重要函数,在历年的高考题中都占据着重要的地位。从近几年的高考形势来看,对指数函数、对数函数、幂函数的考查,大多以基本函数的性质为依托,结合运算推理,能运用它们的性质解决具体问题。为此,我们要熟练掌握指数、对数运算法则,明确算理,能对常见的指数型函数、对数型函数进行变形处理。
预测对本节的考察是:
1.题型有两个选择题和一个解答题;
-
2.题目形式多以指数函数、对数函数、幂函数为载体的复合函数来考察函数的性质。同时它们与其它知识点交汇命题,则难度会加大。
-
1.指数与对数运算
(1)根式的概念:
①定义:若一个数的
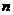 次方等于
次方等于 ,则这个数称
,则这个数称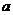 的
的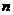 次方根。即若
次方根。即若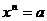 ,则
,则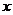 称
称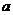 的
的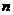 次方根
次方根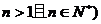 ,
,1)当
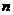 为奇数时,
为奇数时,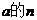 次方根记作
次方根记作 ;
;2)当
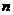 为偶数时,负数
为偶数时,负数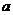 没有
没有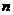 次方根,而正数
次方根,而正数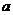 有两个
有两个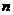 次方根且互为相反数,记作
次方根且互为相反数,记作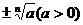 。
。②性质:1)
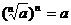 ;2)当
;2)当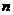 为奇数时,
为奇数时, ;
;3)当
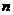 为偶数时,
为偶数时,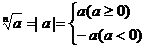 。
。(2).幂的有关概念
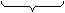 ①规定:1)
①规定:1)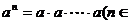 N*;2)
N*;2)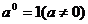 ;
;n个
3)
 Q,4)
Q,4)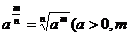 、
、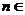 N*
且
N*
且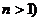 。
。②性质:1)
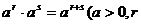 、
、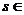 Q);
Q);2)
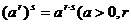 、
、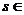 Q);
Q);3)
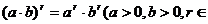 Q)。
Q)。(注)上述性质对r、
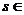 R均适用。
R均适用。(3).对数的概念
①定义:如果
 的b次幂等于N,就是
的b次幂等于N,就是 ,那么数
,那么数 称以
称以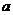 为底N的对数,记作
为底N的对数,记作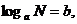 其中
其中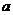 称对数的底,N称真数。
称对数的底,N称真数。1)以10为底的对数称常用对数,
 记作
记作 ;
;2)以无理数
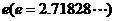 为底的对数称自然对数,
为底的对数称自然对数, ,记作
,记作 ;
;②基本性质:
1)真数N为正数(负数和零无对数);2)
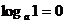 ;
;3)
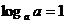 ;4)对数恒等式:
;4)对数恒等式: 。
。③运算性质:如果
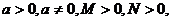 则
则1)
 ;
;2)
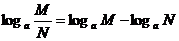 ;
;3)
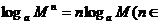 R)。
R)。④换底公式:
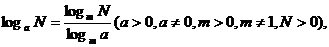
1)
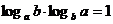 ;2)
;2)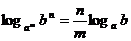 。
。 -
2.指数函数与对数函数
(1)指数函数:
①定义:函数
 称指数函数,
称指数函数,1)函数的定义域为R;2)函数的值域为
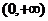 ;
;3)当
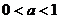 时函数为减函数,当
时函数为减函数,当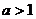 时函数为增函数。
时函数为增函数。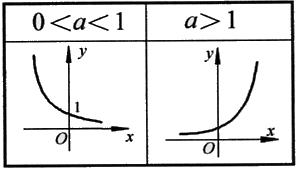 ②函数图像:
②函数图像:1)指数函数的图象都经过点(0,1),且图象都在第一、二象限;
2)指数函数都以
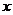 轴为渐近线(当
轴为渐近线(当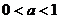 时,图象向左无限接近
时,图象向左无限接近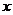 轴,当
轴,当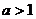 时,图象向右无限接近
时,图象向右无限接近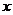 轴);
轴);3)对于相同的
 ,函数
,函数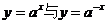 的图象关于
的图象关于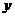 轴对称。
轴对称。
③函数值的变化特征: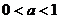
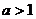
①  ,
,
② ,
,
③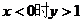
① 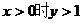 ,
,
② ,
,
③ ,
,
(2)对数函数:
①定义:函数
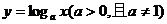 称对数函数,
称对数函数,1)函数的定义域为
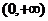 ;2)函数的值域为R;
;2)函数的值域为R;3)当
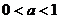 时函数为减函数,当
时函数为减函数,当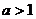 时函数为增函数;
时函数为增函数;4)对数函数
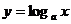 与指数函数
与指数函数 互为反函数。
互为反函数。②函数图像:
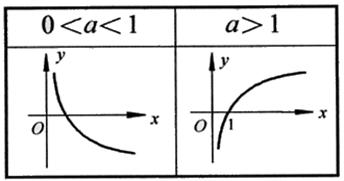
1)对数函数的图象都经过点(0,1),且图象都在第一、四象限;
2)对数函数都以
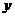 轴为渐近线(当
轴为渐近线(当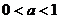 时,图象向上无限接近
时,图象向上无限接近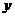 轴;当
轴;当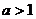 时,图象向下无限接近
时,图象向下无限接近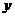 轴);
轴);4)对于相同的
 ,函数
,函数 的图象关于
的图象关于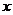 轴对称。
轴对称。③函数值的变化特征:
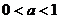
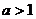
① 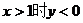 ,
,
② ,
,
③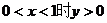 .
.
① 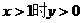 ,
,
② ,
,
③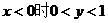 .
.
-
题型1:指数运算
例1.(1)计算:
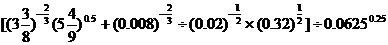 ;
;(2)化简:
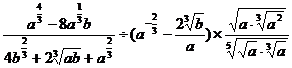 。
。解:(1)原式=
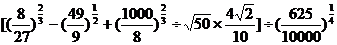
 ;
;(2)原式=
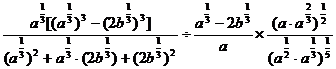
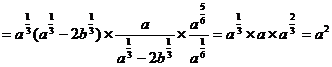 。
。点评:根式的化简求值问题就是将根式化成分数指数幂的形式,然后利用分数指数幂的运算性质求解,对化简求值的结果,一般用分数指数幂的形式保留;一般的进行指数幂运算时,化负指数为正指数,化根式为分数指数幂,化小数为分数运算,同时兼顾运算的顺序。
例2.已知
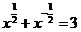 ,求
,求 的值。
的值。解:∵
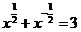 ,
,∴
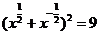 ,
,∴
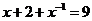 ,
,∴
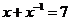 ,
,∴
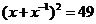 ,
,∴
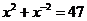 ,
,又∵
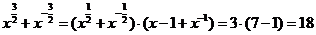 ,
,∴
 。
。点评:本题直接代入条件求解繁琐,故应先化简变形,创造条件简化运算。
题型2:对数运算
例3.计算
(1)
 ;(2)
;(2) ;
;(3)
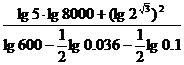 。
。解:(1)原式

 ;
;(2)原式
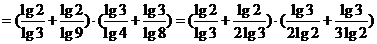
 ;
;(3)分子=
 ;
;分母=
 ;
;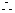 原式=
原式=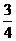 。
。点评:这是一组很基本的对数运算的练习题,虽然在考试中这些运算要求并不高,但是数式运算是学习数学的基本功,通过这样的运算练习熟练掌握运算公式、法则,以及学习数式变换的各种技巧。
例4.设
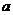 、
、 、
、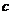 为正数,且满足
为正数,且满足

(1)求证:
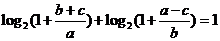 ;
;(2)若
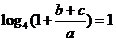 ,
,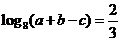 ,求
,求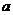 、
、 、
、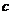 的值。
的值。证明:(1)左边
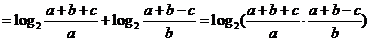
 ;
;解:(2)由
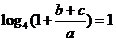 得
得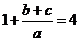 ,
,∴
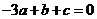 ……………①
……………①由
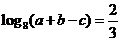 得
得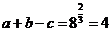 ………… ……………②
………… ……………②由①
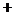 ②得
②得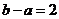 ……………………………………③
……………………………………③由①得
 ,代入
,代入 得
得 ,
,∵
 ,
∴
,
∴ ………………………………④
………………………………④由③、④解得
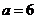 ,
, ,从而
,从而 。
。点评:对于含对数因式的证明和求值问题,还是以对数运算法则为主,将代数式化简到最见形式再来处理即可。
题型3:指数、对数方程
例5.设关于
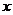 的方程
的方程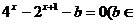 R),
R),(1)若方程有实数解,求实数b的取值范围;
(2)当方程有实数解时,讨论方程实根的个数,并求出方程的解。
解:(1)原方程为
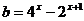 ,
, ,
,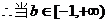 时方程有实数解;
时方程有实数解;(2)①当
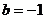 时,
时, ,∴方程有唯一解
,∴方程有唯一解 ;
;②当
 时,
时, .
.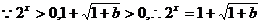 的解为
的解为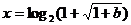 ;
;令
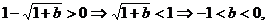
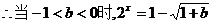 的解为
的解为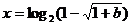 ;
;综合①、②,得
1)当
 时原方程有两解:
时原方程有两解: ;
;2)当
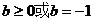 时,原方程有唯一解
时,原方程有唯一解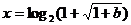 ;
;3)当
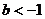 时,原方程无解。
时,原方程无解。点评:具有一些综合性的指数、对数问题,问题的解答涉及指数、对数函数,二次函数、参数讨论、方程讨论等各种基本能力,这也是指数、对数问题的特点,题型非常广泛,应通过解题学习不断积累经验。
例6.(2006辽宁 文13)方程
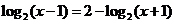 的解为
。
的解为
。解:考察对数运算。原方程变形为
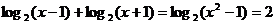 ,即
,即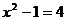 ,得
,得 。且
。且 有
有 。从而结果为
。从而结果为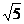 。
。点评:上面两例是关于含指数式、对数式等式的形式,解题思路是转化为不含指数、对数因式的普通等式或方程的形式,再来求解。
题型4:指数函数的概念与性质
例7.设
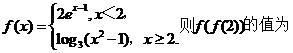 ( )
( )A.0 B.1 C.2 D.3
解:C;
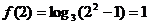 ,
,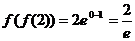 。
。点评:利用指数函数、对数函数的概念,求解函数的值。
例8.已知
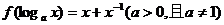 试求函数f(x)的单调区间。
试求函数f(x)的单调区间。解:令
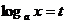 ,则x=
,则x= ,t∈R。
,t∈R。所以
 即
即 ,(x∈R)。
,(x∈R)。因为f(-x)=f(x),所以f(x)为偶函数,故只需讨论f(x)在[0,+∞)上的单调性。
任取
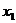 ,
,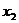 ,且使
,且使 ,则
,则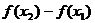
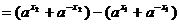
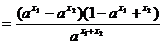
(1)当a>1时,由
 ,有
,有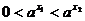 ,
,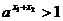 ,所以
,所以 ,即f(x)在[0,+∞]上单调递增。
,即f(x)在[0,+∞]上单调递增。(2)当0<a<1时,由
 ,有
,有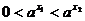 ,
, ,所以
,所以 ,即f(x)在[0,+∞]上单调递增。
,即f(x)在[0,+∞]上单调递增。综合所述,[0,+∞]是f(x)的单调增区间,(-∞,0)是f(x)的单调区间。
点评:求解含指数式的函数的定义域、值域,甚至是证明函数的性质都需要借助指数函数的性质来处理。特别是分
 两种情况来处理。
两种情况来处理。题型5:指数函数的图像与应用
例9.若函数
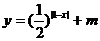 的图象与x轴有公共点,则m的取值范围是( )
的图象与x轴有公共点,则m的取值范围是( )A.m≤-1 B.-1≤m<0 C.m≥1 D.0<m≤1
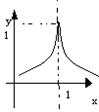 解:
解: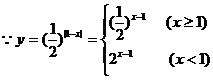 ,
,画图象可知-1≤m<0。
答案为B。
点评:本题考察了复杂形式的指数函数的图像特征,解题的出发点仍然是
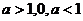 两种情况下函数
两种情况下函数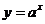 的图像特征。
的图像特征。例10.设函数
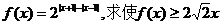 的取值范围。
的取值范围。解:由于
 是增函数,
是增函数, 等价于
等价于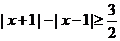 ①
①1)当
 时,
时,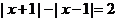 ,
,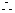 ①式恒成立;
①式恒成立;2)当
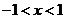 时,
时,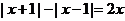 ,①式化为
,①式化为 ,即
,即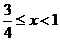 ;
;3)当
 时,
时,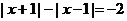 ,①式无解;
,①式无解;综上
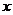 的取值范围是
的取值范围是 。
。点评:处理含有指数式的不等式问题,借助指数函数的性质将含有指数式的不等式转化为普通不等式问题(一元一次、一元二次不等式)来处理。
题型6:对数函数的概念与性质
例11.(1)函数
 的定义域是( )
的定义域是( )A.
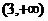 B.
B. C.
C.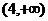 D.
D.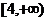
(2)(2006湖北)设f(x)=
 ,则
,则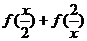 的定义域为( )
的定义域为( )A.
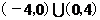 B.(-4,-1)
B.(-4,-1)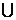 (1,4)
(1,4) C.(-2,-1)
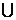 (1,2)
D.(-4,-2)
(1,2)
D.(-4,-2)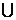 (2,4)
(2,4)解:(1)D(2)B。
点评:求函数定义域就是使得解析是有意义的自变量的取值范围,在对数函数中只有真数大于零时才有意义。对于抽象函数的处理要注意对应法则的对应关系。
例12.对于
 ,
, (1)函数的“定义域为R”和“值域为R”是否是一回事;
(2)结合“实数a的取何值时
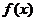 在
在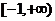 上有意义”与“实数a的取何值时函数的定义域为
上有意义”与“实数a的取何值时函数的定义域为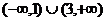 ”说明求“有意义”问题与求“定义域”问题的区别;
”说明求“有意义”问题与求“定义域”问题的区别;(3)结合(1)(2)两问,说明实数a的取何值时
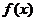 的值域为
的值域为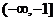
(4)实数a的取何值时
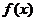 在
在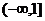 内是增函数。
内是增函数。解:记
 ,则
,则 ;
;(1)不一样;
定义域为R
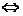
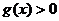 恒成立。
恒成立。得:
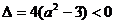 ,解得实数a的取值范围为
,解得实数a的取值范围为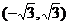 。
。值域为R:
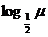 值域为R
值域为R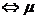 至少取遍所有的正实数,
至少取遍所有的正实数,则
 ,解得实数a的取值范围为
,解得实数a的取值范围为 。
。(2)实数a的取何值时
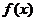 在
在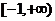 上有意义:
上有意义:命题等价于
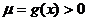 对于任意
对于任意 恒成立,
恒成立,则
 或
或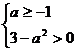 ,
,解得实数a得取值范围为
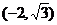 。
。实数a的取何值时函数的定义域为
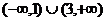 :
:由已知得二次不等式
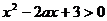 的解集为
的解集为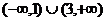 可得
可得 ,则a=2。故a的取值范围为{2}。
,则a=2。故a的取值范围为{2}。区别:“有意义问题”正好转化成“恒成立问题”来处理,而“定义域问题”刚好转化成“取遍所有问题”来解决(这里转化成了解集问题,即取遍解集内所有的数值)
(3)易知
 得值域是
得值域是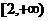 ,又
,又 得值域是
得值域是 ,
,得
 ,故a得取值范围为{-1,1}。
,故a得取值范围为{-1,1}。(4)命题等价于
 在
在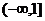 上为减函数,且
上为减函数,且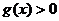 对任意的
对任意的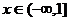 恒成立,则
恒成立,则 ,解得a得取值范围为
,解得a得取值范围为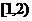 。
。点评:该题主要考察复合对数函数的定义域、值域以及单调性问题。解题过程中遇到了恒成立问题,“恒为正”与“取遍所有大于零的数”不等价,同时又考察了一元二次函数函数值的分布情况,解题过程中结合三个“二次”的重要结论来进行处理。
题型7:对数函数的图像及应用
例13.当a>1时,函数y=logax和y=(1-a)x的图象只可能是( )

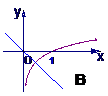

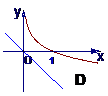
解:当a>1时,函数y=logax的图象只能在A和C中选,
又a>1时,y=(1-a)x为减函数。
答案:B
点评:要正确识别函数图像,一是熟悉各种基本函数的图像,二是把握图像的性质,根据图像的性质去判断,如过定点、定义域、值域、单调性、奇偶性。
例14.设A、B是函数y= log2x图象上两点, 其横坐标分别为a和a+4, 直线l: x=a+2与函数y= log2x图象交于点C, 与直线AB交于点D。
(1)求点D的坐标;
(2)当△ABC的面积大于1时, 求实数a的取值范围。
解:(1)易知D为线段AB的中点, 因A(a, log2a ), B(a+4, log2(a+4)),
所以由中点公式得D(a+2, log2
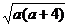 )。
)。(2)S△ABC=S梯形AA′CC′+S梯形CC′B′B- S梯形AA′B′B=…= log2
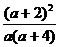 ,
, 其中A′,B′,C′为A,B,C在x轴上的射影。
由S△ABC= log2
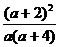 >1, 得0< a<2
>1, 得0< a<2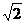 -2。
-2。点评:解题过程中用到了对数函数性质,注意底数分类来处理,根据函数的性质来处理复杂问题。
题型8:指数函数、对数函数综合问题
例15.在xOy平面上有一点列P1(a1,b1),P2(a2,b2),…,Pn(an,bn)…,对每个自然数n点Pn位于函数y=2000(
 )x(0<a<1)的图象上,且点Pn,点(n,0)与点(n+1,0)构成一个以Pn为顶点的等腰三角形。
)x(0<a<1)的图象上,且点Pn,点(n,0)与点(n+1,0)构成一个以Pn为顶点的等腰三角形。(1)求点Pn的纵坐标bn的表达式;
(2)若对于每个自然数n,以bn,bn+1,bn+2为边长能构成一个三角形,求a的取值范围;
(3)设Cn=lg(bn)(n∈N*),若a取(2)中确定的范围内的最小整数,问数列{Cn}前多少项的和最大?试说明理由。
解:(1)由题意知:an=n+
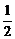 ,∴bn=2000(
,∴bn=2000( )
) 。
。(2)∵函数y=2000(
 )x(0<a<10)递减,
)x(0<a<10)递减,∴对每个自然数n,有bn>bn+1>bn+2。
则以bn,bn+1,bn+2为边长能构成一个三角形的充要条件是bn+2+bn+1>bn,
即(
 )2+(
)2+( )-1>0,
)-1>0,解得a<-5(1+
 )或a>5(
)或a>5(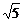 -1)。
-1)。 ∴5(
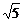 -1)<a<10。
-1)<a<10。(3)∵5(
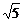 -1)<a<10,∴a=7
-1)<a<10,∴a=7∴bn=2000(
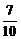 )
) 。数列{bn}是一个递减的正数数列,
。数列{bn}是一个递减的正数数列,对每个自然数n≥2,Bn=bnBn-1。
于是当bn≥1时,Bn<Bn-1,当bn<1时,Bn≤Bn-1,
因此数列{Bn}的最大项的项数n满足不等式bn≥1且bn+1<1,
由bn=2000(
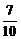 )
) ≥1得:n≤20。
≥1得:n≤20。∴n=20。
点评:本题题设从函数图像入手,体现数形结合的优越性,最终还是根据函数性质结合数列知识,以及三角形的面积解决了实际问题。
例16.已知函数
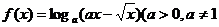 为常数)
为常数)(1)求函数f(x)的定义域;
(2)若a=2,试根据单调性定义确定函数f(x)的单调性。
(3)若函数y=f(x)是增函数,求a的取值范围。
解:(1)由

∵a>0,x≥0
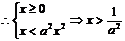
∴f(x)的定义域是
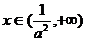 。
。(2)若a=2,则
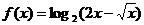
设
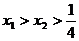 , 则
, 则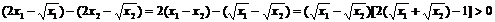

故f(x)为增函数。
(3)设

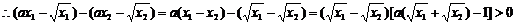
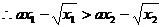 ①
①∵f(x)是增函数,
∴f(x1)>f(x2)
即
 ②
②联立①、②知a>1,
∴a∈(1,+∞)。
点评:该题属于纯粹的研究复合对函数性质的问题,我们抓住对数函数的特点,结合一般函数求定义域、单调性的解题思路,对“路”处理即可。
题型9:课标创新题
例17.对于在区间
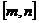 上有意义的两个函数f(x)与g(x),如果对任意的
上有意义的两个函数f(x)与g(x),如果对任意的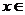
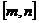 ,均有
,均有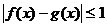 ,则称f(x)与g(x)在
,则称f(x)与g(x)在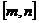 上是接近的,否则称f(x)与g(x)在
上是接近的,否则称f(x)与g(x)在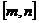 上是非接近的,现有两个函数
上是非接近的,现有两个函数 与
与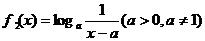 ,给定区间
,给定区间 。
。(1)若
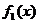 与
与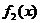 在给定区间
在给定区间 上都有意义,求a的取值范围;
上都有意义,求a的取值范围;(2)讨论
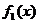 与
与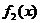 在给定区间
在给定区间 上是否是接近的。
上是否是接近的。解:(1)两个函数
 与
与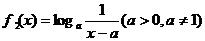 在给定区间
在给定区间 有意义,因为函数
有意义,因为函数 给定区间
给定区间 上单调递增,函数在
上单调递增,函数在 给定区间
给定区间 上恒为正数,
上恒为正数,故有意义当且仅当
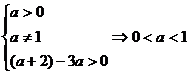 ;
;(2)构造函数
 ,
,对于函数
 来讲,
来讲, 显然其在
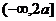 上单调递减,在
上单调递减,在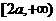 上单调递增。
上单调递增。且
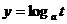 在其定义域内一定是减函数。
在其定义域内一定是减函数。由于
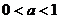 ,得
,得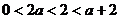
所以原函数在区间
 内单调递减,只需保证
内单调递减,只需保证

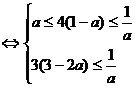
当
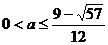 时,
时,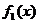 与
与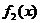 在区间
在区间 上是接近的;
上是接近的;当
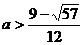
 时,
时,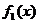 与
与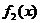 在区间
在区间 上是非接近的。
上是非接近的。点评:该题属于信息给予的题目,考生首先理解“接近”与“非接近”的含义,再对含有对数式的函数的是否“接近”进行研究,转化成含有对数因式的不等式问题,解不等式即可。
例18.设
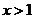 ,
,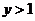 ,且
,且 ,求
,求 的最小值。
的最小值。解:令
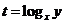 ,
,∵
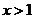 ,
,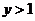 ,∴
,∴ 。
。由
 得
得 ,∴
,∴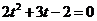 ,
,∴
 ,∵
,∵ ,∴
,∴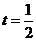 ,即
,即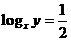 ,∴
,∴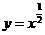 ,
,∴
 ,
,∵
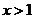 ,∴当
,∴当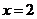 时,
时, 。
。点评:对数函数结合不等式知识处理最值问题,这是出题的一个亮点。同时考察了学生的变形能力。
-
1.
 (其中
(其中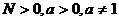 )是同一数量关系的三种不同表示形式,因此在许多问题中需要熟练进行它们之间的相互转化,选择最好的形式进行运算.在运算中,根式常常化为指数式比较方便,而对数式一般应化为同应化为同底;
)是同一数量关系的三种不同表示形式,因此在许多问题中需要熟练进行它们之间的相互转化,选择最好的形式进行运算.在运算中,根式常常化为指数式比较方便,而对数式一般应化为同应化为同底; -
2.要熟练运用初中学习的多项式各种乘法公式;进行数式运算的难点是运用各种变换技巧,如配方、因式分解、有理化(分子或分母)、拆项、添项、换元等等,这些都是经常使用的变换技巧,必须通过各种题型的训练逐渐积累经验;
-
3.解决含指数式或对数式的各种问题,要熟练运用指数、对数运算法则及运算性质,更关键是熟练运用指数与对数函数的性质,其中单调性是使用率比较高的知识;
-
4.指数、对数函数值的变化特点(上面知识结构表中的12个小点)是解决含指数、对数式的问题时使用频繁的关键知识,要达到滚瓜烂熟,运用自如的水平,在使用时常常还要结合指数、对数的特殊值共同分析;
-
5.含有参数的指数、对数函数的讨论问题是重点题型,解决这类问题的最基本的分类方案是以“底”大于1或小于1分类;
-
6.在学习中含有指数、对数的复合函数问题大多数都是以综合形式出现,如与其它函数(特别是二次函数)形成的复合函数问题,与方程、不等式、数列等内容形成的各类综合问题等等,因此要努力提高综合能力。