高考数学二诊文科试题
高考数学二诊文科试题参考答案
理科数学参考答案及评分意见
一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的，把它选出来填涂在答题卡上．
CDACB ACBDA BD
二、填空题：本大题共4小题，每小题4分，共16分．把答案填在题中横线上．
13．
14．b≤
且 b≠0
15．
16．4
三、解答题：本大题共6小题，共74分．解答应写出文字说明、证明过程或演算步骤．
17．由
知B为锐角，得 
，
，
所以 
，得 A + B = 45°，
因此∠C = 135°，表明c边最长． ……………………… 5分
∵ tanA＞tanB，且正切函数在(0°，90°)内单调增加，
∴ A＞B，于是b边最短，即 b = 1．
∵ 
，
∴ 由正弦定理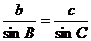
得
，
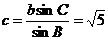故最长边的值为
．
………………………12分
18．设不等式︱2x－4︱＜5－x，
，2x2 + mx－1＜0的解集分别为A，B，C．
则由︱2x－4︱＜5－x得，当x≥2时，不等式化为 2x－4＜5－x，得 x＜3，所以有2≤x＜3；当x＜2时，不等式化为 4－2x＜5－x，得 x＞－1，所以有－1＜x＜2，故A =(－1，3)． …………… 3分
Û 
Û 
Û 
Û 0≤x＜1 或 2＜x≤4，
即 B = [
0，1
∪(2，4
．
…………… 6分
若同时满足①②的x值也满足③，则有A∩BÍC．
设 f(x)= 2x2 +
mx－1，则由于A∩B =
[ 0，1∪(2，3)，
故结合二次函数的图象，得 
．
…………… 12分
19．设开办初中班x个，高中班y个，收取的学费总额为z万元．
根据题意，有 x≥0，y≥0，且x、y∈Z； ①
20≤x + y≤30； ②
25x + 50y + 2.5×3.2x + 4.0×4.0y ≤1320，
即 x + 2y≤40． ③
目标函数为 z = 0.7×40 x + 0.8×45 y = 28 x + 36 y，可行域如图：
…………… 6分
把z = 28 x + 36 y变形为
，
得到斜率为
，在y轴上的截距为
，随z
变化的一簇平行直线．由图象可以看到，当直
线z = 28 x + 36 y经过可行域上的点A时，z最大．
解方程组 
得x
= 20，y = 10，
即点A的坐标为(20，10)，所以 zmax = 28×20 + 36×10 = 920．
由此可知，开办20个初中班和10个高中班，收取的学费总额最多，为920万元． …………… 12分
20． (Ⅰ) ∵ f(x)= x3 +(m2－4m + 2)x + m3－6m2 + 9m－1，
∴ f ′(x)= 3x2 +(m2－4m + 2)．
因为f(x)有极值，故 f ′(x)= 0有两个不同的实数根，
∴ m2－4m + 2＜0，
∴ 
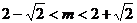． ……………… 4分
(Ⅱ)设 f ′(x)= 0的实数根为a，b(a＜b)，则 a +b = 0．
于是 g(m)= f(a)+ f(b)
= a3 + b3 +(m2－4m + 2)(a + b)+ 2(m3－6m2 + 9m－1)
=(a + b)(a2－ab + b2)+(m2－4m－2)(a + b)+ 2(m3－6m2 + 9m－1)，
由 a +b = 0 得 g(m)= 2(m3－6m2 + 9m－1)，()．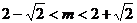
……………… 8分
∴ g ′(m)= 6(m2－4m + 3)，由 g ′(m)= 0，得 m = 1，3．
|
m |
 |
… |
1 |
… |
3 |
… |
 |
|
g ′(m) |
|
+ |
0 |
－ |
0 |
+ |
|
|
g(m) |
 |
 |
6 |
 |
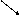－2 |
 |
 |
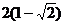由上表得，最大值 g(1)= 6，最小值 g(3)=－2． …………12分
21．设直线FA的斜率为k，其方程为y = kx + 1． ①
因为点A(x，y)同时满足式①和圆，所以把式①代入圆的方程中，得 (x－3)2 +(kx + 1)2 = 1，
即 (1 + k2)x2－(6－2k)x + 9 = 0．
其根的判别式 △ =(6－2k)2－4 . 9 .(1 + k2)≥0，
解得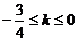 
．
② ……… 3分
设 
、
，把式①代入抛物线方程中，得
，即
x2－4kx－4 = 0．
③
显然△ =(4k)2－4×1×(－4)= 16(k2 + 1)＞0，xB，xC是方程③的两个实数根，
有 xB + xC = 4k，xB . xC =－4． ④ ……… 6分
于是切线CP、BP的方程为
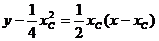， ⑤
， ⑥
由⑤－⑥得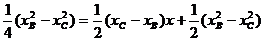 
，
∴ 
，
=
．
于是CP与BP的交点为P(2k，－1)，即点P的轨迹为一条水平线段，其轨迹方程为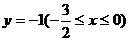
．
……………… 12分
22． (Ⅰ)当n≥2时，由已知式子，得 an [ an－(2n－1)] = an－1(a n－1 + 2n－1)，
整理，得 an 2－an－12 =(2n－1)(an + a n－1)．
因为 { an } 是正项数列，所以 an + a n－1 ≠0，
故只有 an = an－1 + 2n－1． …………2分
于是，当n≥2时， a2 = a1 + 2×1，
a3 = a2 + 2×1，
……
an = an－1 + 2n－1，
上面n－1个式子相加得 an－a1 = 2(2 + 3 + … + n)－(n－1)，
解得 an = n2．
又当 n = 1时，a1 = 1满足上式，故an = n2． …………5分
(Ⅱ)
，
，
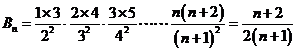…………7分
当n = 1时，
；当n = 2时，
；当n = 3时，
； 猜想当n≥3时，
．
…………9分
以下用数学归纳法证明：
① 当n
= 3时，左边
右边，命题成立．
② 假设当n
= k(k≥3)时，
，即
．
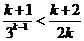当n = k + 1时，
(因为
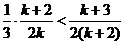Û
(k + 2)2 ＜3 k(k + 3)Û 2k2－4k + 5＞0 Û 2(k－1)2 + 3＞0)，命题成立．
故当n≥3时，．
综上所述，当n = 1时，
，n = 2时，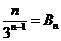
，当n≥3时，．
…………14分