-
(1)设集合M={4,5,6,8},集合N={3,5,7,8}那么M∪N=
(A){3,4,5,6,7,8} (B){5,8} (C){3,5,7,8} (D){4,5,6,8}
 (2)函数f(x)=1+log2x与g(x)=2-x+1在同一直角坐标系下的图象大致是
(2)函数f(x)=1+log2x与g(x)=2-x+1在同一直角坐标系下的图象大致是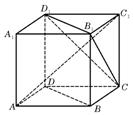 (3)某商场买来一车苹果,从中随机抽取了10个苹果,其重量(单位:克)分别为:150,152,153,
(3)某商场买来一车苹果,从中随机抽取了10个苹果,其重量(单位:克)分别为:150,152,153,149,148,146,151,150,152,147,由此估计这车苹果单个重量的期望值是
(A)150.2克 (B)149.8克 (C)149.4克 (D)147.8克
(4)如图,ABCD-A1B1C1D1为正方体,下面结论错误的是
(A)BD∥平面CB1D1 (B)AC1⊥BD
(C)AC1⊥平面CB1D1 (D)异面直线AD与CB所成的角为60°
(5)如果双曲线
 =1上一点P到双曲线右焦点的距离是2,那么点P到y轴的距离是
=1上一点P到双曲线右焦点的距离是2,那么点P到y轴的距离是 (A)
(A) (B)
(B) (C)
(C)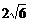 (D)
(D)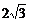
(6)设球O的半径是1,A、B、C是球面上三点,已知A到B、C两点的
球面距离都是
 ,且二面角B-OA-C的大小是
,且二面角B-OA-C的大小是 ,则从A点沿球面经B、C
,则从A点沿球面经B、C两点再回到A点的最短距离是
(A)
 (B)
(B) (C)
(C) (D)
(D)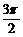
(7)等差数列{an}中,a1=1,a3+a5=14,其降n项和Sn=100,则n=
(A)9 (B)10 (C)11 (D)12
(8)设A(a,1),B(2,b),C(4,5)为坐标平面上三点,O为坐标原点,若OA与OB在OC方向上的投影相同,则a与b满足的关系式为
A.4a-5b=3 B.5a-4b=3 C.4a+5b=14 D.5a+4b=12
(9)用数字1,2,3,4,5可以组成没有重复数字,并且比20 000大的五位偶数共有
A.48个 B.36个 C.24个 D.18个
(10)已知抛物线y-x2+3上存在关于直线x+y=0对称的相异两点A、B,则|AB|等于
A.3 B.4 C.3
 D.4
D.4
(11)某公司有60万元资金,计划投资甲、乙两个项目,按要求对项目甲的投资不小于对项目乙投资的
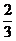 倍,且对每个项目的投资不能低于5万元,对项目甲每投资1万元可获得0.4万元的利润,对项目乙每投资1万元可获得0.6万元的利润,该公司正确提财投资后,在两个项目上共可获得的最大利润为
倍,且对每个项目的投资不能低于5万元,对项目甲每投资1万元可获得0.4万元的利润,对项目乙每投资1万元可获得0.6万元的利润,该公司正确提财投资后,在两个项目上共可获得的最大利润为 A.36万元
B.31.2万元 C.30.4万元
D.24万元
A.36万元
B.31.2万元 C.30.4万元
D.24万元(12)如图,l1、l2、l3是同一平面内的三条平行直线,l1与l2与l3同的距离是2,
正三角形ABC的三顶点分别在l1、l2、l3上,则△ABC的边长是
A.2
 B.
B. C.
C.  D.
D.
-
(13).
 的展开式中的第5项为常数项,那么正整数
的展开式中的第5项为常数项,那么正整数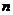 的值是
.
的值是
. -
(17)(本小题满分12分)
厂家在产品出厂前,需对产品做检验,厂家对一般产品致冷商家的,商家符合规定拾取一定数量的产品做检验,以决定是否验收这些产品.
(Ⅰ)若厂家库房中的每件产品合格的概率为0.3,从中任意取出4种进行检验,求至少要1件是合格产品的概率.
(Ⅱ)若厂家发给商家20件产品,其中有3件不合格,按合同规定该商家从中任取2件,来进行检验,只有2件产品合格时才接收这些产品,否则拒收,分别求出该商家计算出不合格产品为1件和2件的概率,并求该商家拒收这些产品的概率。
(18)(本小题满分12分)
已知cosα=
 ,cos(α-β)=
,cos(α-β)=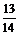 ,且0<β<α<
,且0<β<α< ,
,(Ⅰ)求tan2α的值;
(Ⅱ)求β.
(19) (本小题满分12分)
 如图,平面PCBM⊥平面ABC,∠PCB=90°,PM∥BC,直线AM与直线PC所成的角为60°,又AC=1,BC=2PM=2,∠ACB=90°
如图,平面PCBM⊥平面ABC,∠PCB=90°,PM∥BC,直线AM与直线PC所成的角为60°,又AC=1,BC=2PM=2,∠ACB=90°
(Ⅰ)求证:AC⊥BM;
(Ⅱ)求二面角M-AB-C的大小;
(Ⅲ)求多面体PMABC的体积.
(20)(本小题满分12分)
设函数f(x)=ax3+bx+c(a≠0)为奇函数,其图象在点(1,f(1))处的切线与直线x-6y-7=0垂直,导函数f'(x)的最小值为-12.
(Ⅰ)求a,b,c的值;
(Ⅱ)求函数f(x)的单调递增区间,并求函数f(x)在(-1,3)上的最大值和最小值.
(21)(本小题满分12分)
求F1、F2分别是横线
 的左、右焦点.
的左、右焦点.(Ⅰ)若r是第一象限内该数轴上的一点,
 ,求点P的作标;
,求点P的作标;(Ⅱ)设过定点M(0,2)的直线l与椭圆交于同的两点A、B,且∠ADB为锐角(其中O为作标原点),求直线
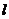 的斜率
的斜率 的取值范围.
的取值范围.(22)(本小题满分14分)
已知函数f(x)=x2-4,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,u)(u,N +),其中为正实数.
(Ⅰ)用xx表示xn+1;
(Ⅱ)若a1=4,记an=lg
 ,证明数列{a1}成等比数列,并求数列{xn}的通项公式;
,证明数列{a1}成等比数列,并求数列{xn}的通项公式;(Ⅲ)若x1=4,bn=xn-2,Tn是数列{bn}的前n项和,证明Tn<3.
(含详细解析)
-
1、设集合
 ,集合
,集合 ,那么
,那么 ( )
( )(A)
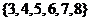 (B)
(B) (C)
(C) (D)
(D)
解析:选A.
-
2、函数
 与
与 在同一直角坐标系下的图象大致是( )
在同一直角坐标系下的图象大致是( )
解析:选C.
-
3、某商场买来一车苹果,从中随机抽取了10个苹果,其重量(单位:克)分别为:150,152,153,149,148,146,151,150,152,147,由此估计这车苹果单个重量的期望值是( )
 (A)150.2克 (B)149.8克 (C)149.4克 (D)147.8克
(A)150.2克 (B)149.8克 (C)149.4克 (D)147.8克解析:选B.
-
4、如图,
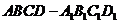 为正方体,下面结论错误的是( )
为正方体,下面结论错误的是( )(A)
 平面
平面
(B)
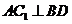
(C)
 平面
平面
(D)异面直线
 与
与 所成的角为60°
所成的角为60°解析:选D.
-
5、如果双曲线
 上一点
上一点 到双曲线右焦点的距离是2,那么点
到双曲线右焦点的距离是2,那么点 到
到 轴的距离是( )
轴的距离是( )(A)
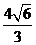 (B)
(B) (C)
(C) (D)
(D)
解析:选A.由点
 到双曲线右焦点
到双曲线右焦点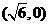 的距离是2知
的距离是2知 在双曲线右支上.又由双曲线的第二定义知点
在双曲线右支上.又由双曲线的第二定义知点 到双曲线右准线的距离是
到双曲线右准线的距离是 ,双曲线的右准线方程是
,双曲线的右准线方程是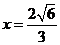 ,故点
,故点 到
到 轴的距离是
轴的距离是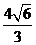 .
. -
6、
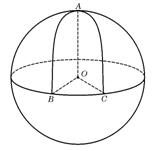 设球
设球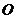 的半径是1,
的半径是1, 、
、 、
、 是球面上三点,已知
是球面上三点,已知 到
到 、
、 两点的球面距离都是
两点的球面距离都是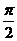 ,且二面角
,且二面角 的大小是
的大小是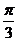 ,则从
,则从 点沿球面经
点沿球面经 、
、 两点再回到
两点再回到 点的最短距离是( )
点的最短距离是( )(A)
 (B)
(B)
(C)
 (D)
(D)
解析:选C.
 .本题考查球面距离.
.本题考查球面距离. -
7、等差数列
 中,
中, ,
, ,其前
,其前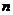 项和
项和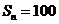 ,则
,则 ( )
( )(A)9 (B)10 (C)11 (D)12
解析:选B.
-
8、设
 ,
, ,
, 为坐标平面上三点,
为坐标平面上三点,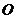 为坐标原点,若
为坐标原点,若 与
与 在
在 方向上的投影相同,则
方向上的投影相同,则 与
与 满足的关系式为( )
满足的关系式为( )(A)
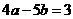 (B)
(B)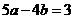 (C)
(C)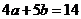 (D)
(D)
解析:选A.由
 与
与 在
在 方向上的投影相同,可得:
方向上的投影相同,可得: 即
即
 ,
,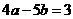 .
. -
9、用数字1,2,3,4,5可以组成没有重复数字,并且比20000大的五位偶数共有( )
(A)48个 (B)36个 (C)24个 (D)18个
解析:选B.个位是2的有
 个,个位是4的有
个,个位是4的有 个,所以共有36个.
个,所以共有36个. -
10、已知抛物线
 上存在关于直线
上存在关于直线 对称的相异两点
对称的相异两点 、
、 ,则
,则 等于( )
等于( )(A)3 (B)4 (C)
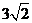 (D)
(D)
解析:选C.设直线
 的方程为
的方程为 ,由
,由 ,进而可求出
,进而可求出 的中点
的中点 ,又由
,又由 在直线
在直线 上可求出
上可求出 ,∴
,∴ ,由弦长公式可求出
,由弦长公式可求出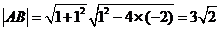 .本题考查直线与圆锥曲线的位置关系.自本题起运算量增大.
.本题考查直线与圆锥曲线的位置关系.自本题起运算量增大. -
11、某公司有60万元资金,计划投资甲、乙两个项目,按要求对项目甲的投资不小于对项目乙投资的
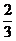 倍,且对每个项目的投资不能低于5万元,对项目甲每投资1万元可获得0.4万元的利润,对项目乙每投资1万元可获得0.6万元的利润,该公司正确规划投资后,在这两个项目上共可获得的最大利润为( )
倍,且对每个项目的投资不能低于5万元,对项目甲每投资1万元可获得0.4万元的利润,对项目乙每投资1万元可获得0.6万元的利润,该公司正确规划投资后,在这两个项目上共可获得的最大利润为( )(A)36万元 (B)31.2万元 (C)30.4万元 (D)24万元
解析:选B.对甲项目投资24万元,对乙项目投资36万元,可获最大利润31.2万元.因为对乙项目投资获利较大,故在投资规划要求内(对项目甲的投资不小于对项目乙投资的
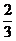 倍)尽可能多地安排资金投资于乙项目,即对项目甲的投资等于对项目乙投资的
倍)尽可能多地安排资金投资于乙项目,即对项目甲的投资等于对项目乙投资的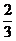 倍时可获最大利润.这是最优解法.也可用线性规划的通法求解.注意线性规划在高考中以应用题型的形式出现.
倍时可获最大利润.这是最优解法.也可用线性规划的通法求解.注意线性规划在高考中以应用题型的形式出现. -
12、
 如图,
如图, 、
、 、
、 是同一平面内的三条平行直线,
是同一平面内的三条平行直线, 与
与 间的距离是1,
间的距离是1, 与
与 间的距离是2,正三角形
间的距离是2,正三角形 的三顶点分别在
的三顶点分别在 、
、 、
、 上,则⊿
上,则⊿ 的边长是( )
的边长是( )(A)2
 (B)
(B)
(C)
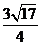 (D)
(D)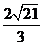
解析:选D.过点C作
 的垂线
的垂线 ,以
,以 、
、 为
为 轴、
轴、 轴建立平面直角坐标系.设
轴建立平面直角坐标系.设 、
、 、
、 ,由
,由 知
知 ,检验A:
,检验A: ,无解;检验B:
,无解;检验B: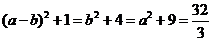 ,无解;检验D:
,无解;检验D: ,正确.本题是把关题.在基础中考能力,在综合中考能力,在应用中考能力,在新型题中考能力全占全了.是一道精彩的好题.可惜区分度太小.
,正确.本题是把关题.在基础中考能力,在综合中考能力,在应用中考能力,在新型题中考能力全占全了.是一道精彩的好题.可惜区分度太小. -
13、
 的展开式中的第5项为常数项,那么正整数
的展开式中的第5项为常数项,那么正整数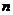 的值是 .
的值是 .解析:
 .
. -
14、在正三棱柱
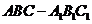 中,侧棱长为
中,侧棱长为 ,底面三角形的边长为1,则
,底面三角形的边长为1,则 与侧面
与侧面 所成的角是____________
所成的角是____________解析:
 ,点
,点 到平面
到平面 的距离为
的距离为 ,∴
,∴ ,
,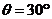 .
. -
15、已知
 的方程是
的方程是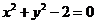 ,
, 的方程是
的方程是 ,由动点
,由动点 向
向 和
和 所引的切线长相等,则运点
所引的切线长相等,则运点 的轨迹方程是__________________
的轨迹方程是__________________解析:
 :圆心
:圆心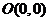 ,半径
,半径 ;
; :圆心
:圆心 ,半径
,半径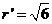 .设
.设 ,由切线长相等得
,由切线长相等得
 ,
,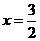 .
. -
16、下面有5个命题:
①函数
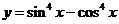 的最小正周期是
的最小正周期是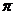 ;
;②终边在
 轴上的角的集合是
轴上的角的集合是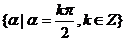 ;
;③在同一坐标系中,函数
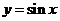 的图象和函数
的图象和函数 的图象有3个公共点;
的图象有3个公共点;④把函数
 的图象向右平移
的图象向右平移 得到
得到 的图象;
的图象;⑤角
 为第一象限角的充要条件是
为第一象限角的充要条件是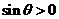
其中,真命题的编号是___________(写出所有真命题的编号)
解析:①
 ,正确;②错误;③
,正确;②错误;③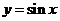 ,
, 和
和 在第一象限无交点,错误;④正确;⑤错误.故选①④.
在第一象限无交点,错误;④正确;⑤错误.故选①④. -
17、(本小题满分12分)厂家在产品出厂前,需对产品做检验,厂家将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收这些产品.
(Ⅰ)若厂家库房中的每件产品合格的概率为0.8,从中任意取出4种进行检验,求至少要1件是合格产品的概率.
(Ⅱ)若厂家发给商家20件产品,其中有3件不合格,按合同规定该商家从中任取2件,来进行检验,只有2件产品合格时才接收这些产品,否则拒收,分别求出该商家计算出不合格产品为1件和2件的概率,并求该商家拒收这些产品的概率。
解析:本题考查相互独立事件、互斥事件等的概率计算,考查运用所学知识与方法解决实际问题的能力.
(Ⅰ)记“厂家任取4件产品检验,其中至少有1件是合格品”为事件
 .用对立事件
.用对立事件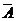 来算,有
来算,有
(Ⅱ)记“商家任取2件产品检验,其中不合格产品数为
 件”
件”
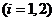 为事件
为事件 .
.

∴商家拒收这批产品的概率
 .
.故商家拒收这批产品的概率为
 .
. -
18、(本小题满分12分)已知
 ,
,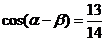 ,且
,且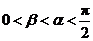 .
.(Ⅰ)求
 的值;
的值;(Ⅱ)求
 .
.解析:本题考查三角恒等变形的主要基本公式、三角函数值的符号、已知三角函数值求角以及计算能力.
(Ⅰ)由
 ,
,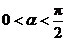 ,得
,得 .
.∴
 .
.于是
 .
.(Ⅱ)由
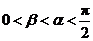 ,得
,得 .
.又∵
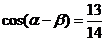 ,
,∴
 .
.由
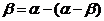 ,得
,得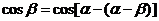
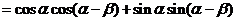

∴
 .
. -
19、
 (本小题满分12分)如图,平面
(本小题满分12分)如图,平面 平面
平面 ,
,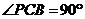 ,
, ,直线
,直线 与直线
与直线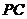 所成的角为60°,又
所成的角为60°,又 ,
, ,
,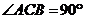 .
.(Ⅰ)求证:
 ;
;(Ⅱ)求二面角
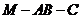 的大小;
的大小;(Ⅲ)求多面体
 的体积.
的体积.解析:本题主要考查异面直线所成的角、平面与平面垂直、二面角、棱锥体积等有关知识,考查思维能力和空间想象能力、应用向量知识解决数学问题的能力、化归转化能力和推理运算能力.
(Ⅰ)∵平面
 平面
平面 ,
, ,
, 平面
平面 .
.∴
 平面
平面
又∵
 平面
平面
∴

(Ⅱ)取
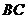 的中点
的中点 ,则
,则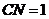 .连接
.连接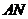 、
、 .
.∵平面
 平面
平面 ,平面
,平面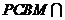 平面
平面 ,
,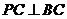 .
.∴
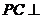 平面
平面 .
.∵
 ,∴
,∴ ,从而
,从而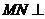 平面
平面 .
.作
 于
于 ,连结
,连结 ,则由三垂线定理知
,则由三垂线定理知 .
.从而
 为二面角
为二面角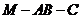 的平面角.
的平面角.∵直线
 与直线
与直线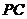 所成的角为60°,
所成的角为60°,∴
 .
.在
 中,由勾股定理得
中,由勾股定理得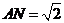 .
.在
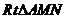 中,
中, .
.在
 中,
中,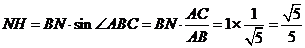 .
.在
 中,
中,
故二面角
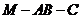 的大小为
的大小为
(Ⅱ)如图以
 为原点建立空间直角坐标系
为原点建立空间直角坐标系 .
.设
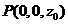
 ,
,有
 ,
, ,
, .
. ,
,
由直线
 与直线
与直线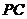 所成的角为60°,得
所成的角为60°,得
即
 ,解得
,解得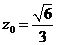 .
.∴
 ,
,
设平面
 的一个法向量为
的一个法向量为 ,则
,则由
 ,取
,取 ,得
,得
取平面
 的一个法向量为
的一个法向量为
则
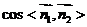

由图知二面角
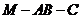 为锐二面角,故二面角
为锐二面角,故二面角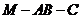 的大小为
的大小为 .
.(Ⅲ)多面体
 就是四棱锥
就是四棱锥
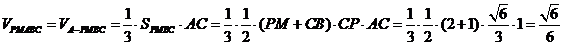 .
. -
20、(本小题满分12分)设函数
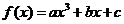
 为奇函数,其图象在点
为奇函数,其图象在点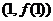 处的切线与直线
处的切线与直线 垂直,导函数
垂直,导函数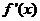 的最小值为
的最小值为 .
.(Ⅰ)求
 ,
, ,
, 的值;
的值;(Ⅱ)求函数
 的单调递增区间,并求函数
的单调递增区间,并求函数 在
在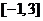 上的最大值和最小值.
上的最大值和最小值.解析:本题考查函数的奇偶性、单调性、二次函数的最值、导数的应用等基础知识,以及推理能力和运算能力.
(Ⅰ)∵
 为奇函数,
为奇函数,∴

即
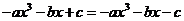
∴

∵
 的最小值为
的最小值为
∴

又直线
 的斜率为
的斜率为
因此,
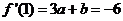
∴
 ,
, ,
, .
.(Ⅱ)
 .
. ,列表如下:
,列表如下:


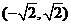


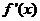
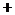



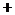


极大

极小

所以函数
 的单调增区间是
的单调增区间是 和
和
∵
 ,
, ,
,
∴
 在
在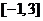 上的最大值是
上的最大值是 ,最小值是
,最小值是 .
. -
21、(本小题满分12分)设
 、
、 分别是椭圆
分别是椭圆 的左、右焦点.
的左、右焦点.(Ⅰ)若
 是第一象限内该椭圆上的一点,且
是第一象限内该椭圆上的一点,且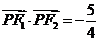 ,求点
,求点 的作标;
的作标;(Ⅱ)设过定点
 的直线
的直线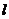 与椭圆交于同的两点
与椭圆交于同的两点 、
、 ,且
,且 为锐角(其中
为锐角(其中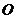 为作标原点),求直线
为作标原点),求直线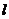 的斜率
的斜率 的取值范围.
的取值范围.解析:本题主要考查直线、椭圆、平面向量的数量积等基础知识,以及综合运用数学知识解决问题及推理计算能力.
(Ⅰ)易知
 ,
, ,
, .
.∴
 ,
,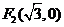 .设
.设
 .则
.则 ,又
,又 ,
,联立
 ,解得
,解得 ,
, .
.(Ⅱ)显然
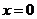 不满足题设条件.可设
不满足题设条件.可设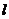 的方程为
的方程为 ,设
,设 ,
, .
.联立

∴
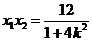 ,
,
由

 ,
, ,得
,得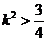 .①
.①又
 为锐角
为锐角 ,
,∴
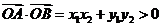
又

∴





∴
 .②
.②综①②可知
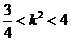 ,∴
,∴ 的取值范围是
的取值范围是 .
. -
22、(本小题满分14分)已知函数
 ,设曲线
,设曲线 在点
在点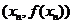 处的切线与
处的切线与 轴的交点为
轴的交点为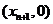
 ,其中
,其中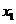 为正实数.
为正实数.(Ⅰ)用
 表示
表示 ;
;(Ⅱ)若
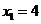 ,记
,记 ,证明数列
,证明数列 成等比数列,并求数列
成等比数列,并求数列 的通项公式;
的通项公式;(Ⅲ)若
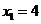 ,
, ,
, 是数列
是数列 的前
的前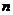 项和,证明
项和,证明 .
.解析:本题综合考查数列、函数、不等式、导数应用等知识,以及推理论证、计算及解决问题的能力.
(Ⅰ)由题可得
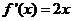 .
.所以曲线
 在点
在点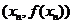 处的切线方程是:
处的切线方程是: .
.即
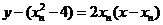 .
.令
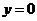 ,得
,得 .
.即
 .
.显然
 ,∴
,∴ .
.(Ⅱ)由
 ,知
,知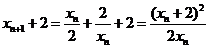 ,同理
,同理 .
.故
 .
.从而
 ,即
,即 .所以,数列
.所以,数列 成等比数列.
成等比数列.故
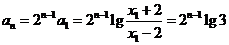 .
.即
 .
.从而

所以

(Ⅲ)由(Ⅱ)知
 ,
,∴

∴

当
 时,显然
时,显然 .
.当
 时,
时,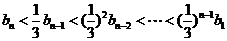
∴


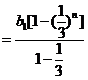
 .
.综上,

 .
.