18．
小型交流发电机中，矩形金属线圈在匀强磁场中匀速转动，产生的感应电动势与时间呈正弦函数关系，如图所示，此线圈与一个R=10Ω的电阻构成闭合电路．不计电路的其他电阻．下列说法正确的是（ ）
小型交流发电机中，矩形金属线圈在匀强磁场中匀速转动，产生的感应电动势与时间呈正弦函数关系，如图所示，此线圈与一个R=10Ω的电阻构成闭合电路．不计电路的其他电阻．下列说法正确的是（ ）| A． | 交变电流的周期为0.125s | B． | 交变电流的频率为4Hz | ||
| C． | 交变电流的有效值为$\sqrt{2}$A | D． | 交变电流的最大值为4A |
17．
如图所示，一理想变压器原线圈匝数为n1=1000匝，副线圈匝数为n2=200匝，将原线圈接在u=200$\sqrt{2}$sin120πt（V）的交流电压上，电阻R=100Ω，电流表A为理想电表．下列推断正确的是（ ）
如图所示，一理想变压器原线圈匝数为n1=1000匝，副线圈匝数为n2=200匝，将原线圈接在u=200$\sqrt{2}$sin120πt（V）的交流电压上，电阻R=100Ω，电流表A为理想电表．下列推断正确的是（ ）| A． | 交变电流的频率为50 Hz | |
| B． | 穿过铁芯的磁通量的最大变化率为$\frac{\sqrt{2}}{25}$Wb/s | |
| C． | 电流表A的示数为$\frac{2\sqrt{2}}{5}$A | |
| D． | 变压器的输入功率是16 W |
16．
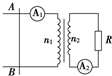如图所示，理想变压器原、副线圈匝数之比n1：n2=4：1，原线圈两端连接光滑导轨，副线圈与电阻R相连组成闭合回路．当直导线AB在匀强磁场中沿导轨匀速地向左做切割磁感线运动时，安培表A1的读数是12mA，那么安培表A2的读数是（ ）
如图所示，理想变压器原、副线圈匝数之比n1：n2=4：1，原线圈两端连接光滑导轨，副线圈与电阻R相连组成闭合回路．当直导线AB在匀强磁场中沿导轨匀速地向左做切割磁感线运动时，安培表A1的读数是12mA，那么安培表A2的读数是（ ）| A． | 0 | B． | 3mA | C． | 48 mA | D． | 无法确定 |
15．如图所示为一交变电流随时间变化的图象，此交流电电流的有效值为（ ）
| A． | 5$\sqrt{2}$ A | B． | 5 A | C． | 3.5$\sqrt{2}$ A | D． | 3.5 A |
14．下列有关物理学史的说法中正确的是（ ）
| A． | 法拉第发现了电流的磁效应 | |
| B． | 奥斯特发现了电磁感应定律 | |
| C． | 库仑发现了点电荷间的作用规律 | |
| D． | 洛伦兹发现了磁场对电流的作用规律 |
如图所示，用质量为m、电阻为R的均匀导线做成边长为l的单匝正方形线框MNPQ，线框每一边的电阻都相等．将线框置于光滑绝缘的水平面上．在线框的右侧存在竖直方向的有界匀强磁场，磁场边界间的距离为2l，磁感应强度为B．在垂直MN边的水平拉力作用下，线框以垂直磁场边界的速度v匀速穿过磁场．在运动过程中线框平面水平，且MN边与磁场的边界平行．求：
12．下列说法正确的是（ ）
| A． | 氢原子从高能级向低能级跃迁的过程中释放的光子的能量有可能大于13.6eV | |
| B． | 物质波就是任何一个运动着的物体都有一种波与它对应，该波的波长与该物体的动量成反比 | |
| C． | 在探究光电效应的实验中，若入射光的强度越强，则光电流就越大 | |
| D． | 光在传播过程中主要表现为波动性而在与物体发生相互作用时主要表现为粒子性 |
如图所示，单摆摆长L=1.0m，C点在悬点O的正下方，D点与C点相距为x=0.6m，C、D之间是光滑绝缘水平面，当摆球A（不带电）运动至左侧最大位移处时，带电小球B从D点由静止释放，小球B的电荷量q=+2.0×10-2C．A、B的质量均为m=200g．当小球B运动到C点时，A、B小球恰在C点迎面相碰．（A、B小球均看成质点，不计空气阻力，计算时取g=10m/s2，π2=10）．求
如图所示，一截面为直角三角形的玻璃砖ABC，∠A=30°，一条与AC边成45°角的光线从AC边的中点D点射入玻璃砖，经AB边反射后的反射光线从BC边的E点垂直于BC边射出．已知AC边长l=0.2m，真空中的光速c=3.0×108m/s，取$\sqrt{2}$=1.4．求
9．
在做“用单摆测定重力加速度”的实验中．
（1）如果测得的g值偏大，可能的原因是D（填写字母代号）
A．测摆长时，忘记了摆球的半径
B．摆线上端悬点未固定牢，摆动中出现松动，使摆线长度增加了
C．开始计时时，秒表过早按下
D．实验中误将49次全振动次数记为50次
（2）某同学在实验中，测量6种不同摆长l情况下单摆的振动周期T，记录实验数据如下：
请以l为横坐标，T2为纵坐标，在如图1中作出T2-l图线，并利用此图线得重力加速度g=9.86m/s2．（取π2=9.86，结果保留三位有效数字）
（3）一位同学查阅资料得知，单摆在最大摆角θ较大时周期公式可近似表述为T=2π（1+$\frac{1}{4}$sin2$\frac{θ}{2}$）$\sqrt{\frac{l}{g}}$．为了用图象法验证单摆周期T和最大摆角θ的关系，他测出摆长为l的同一单摆在不同最大摆角θ时的周期T，并根据实验数据描绘出如图2所示的图线．根据所给周期公式可知，图中的纵轴表示的是sin2$\frac{θ}{2}$，图线延长后与横轴交点的横坐标为$2π\sqrt{\frac{l}{g}}$．
0 144425 144433 144439 144443 144449 144451 144455 144461 144463 144469 144475 144479 144481 144485 144491 144493 144499 144503 144505 144509 144511 144515 144517 144519 144520 144521 144523 144524 144525 144527 144529 144533 144535 144539 144541 144545 144551 144553 144559 144563 144565 144569 144575 144581 144583 144589 144593 144595 144601 144605 144611 144619 176998
在做“用单摆测定重力加速度”的实验中．（1）如果测得的g值偏大，可能的原因是D（填写字母代号）
A．测摆长时，忘记了摆球的半径
B．摆线上端悬点未固定牢，摆动中出现松动，使摆线长度增加了
C．开始计时时，秒表过早按下
D．实验中误将49次全振动次数记为50次
（2）某同学在实验中，测量6种不同摆长l情况下单摆的振动周期T，记录实验数据如下：
| l/m | 0.4 | 0.5 | 0.8 | 0.9 | 1.0 | 1.2 |
| T/s | 1.26 | 1.42 | 1.79 | 1.90 | 2.00 | 2.20 |
| T2/s2 | 1.59 | 2.02 | 3.20 | 3.61 | 4.00 | 4.84 |
（3）一位同学查阅资料得知，单摆在最大摆角θ较大时周期公式可近似表述为T=2π（1+$\frac{1}{4}$sin2$\frac{θ}{2}$）$\sqrt{\frac{l}{g}}$．为了用图象法验证单摆周期T和最大摆角θ的关系，他测出摆长为l的同一单摆在不同最大摆角θ时的周期T，并根据实验数据描绘出如图2所示的图线．根据所给周期公式可知，图中的纵轴表示的是sin2$\frac{θ}{2}$，图线延长后与横轴交点的横坐标为$2π\sqrt{\frac{l}{g}}$．