6. 为了科学研究的需要,常常将质子(带有一个正的元电荷,质量为一个原子质量单位)和α粒子(带有两个正的元电荷,质量为四个原子质量单位)等带电粒子贮存在圆环状空腔中,圆环状空腔置于一个与圆环平面垂直的匀强磁场中,带电粒子在其中做匀速圆周运动(如图).如果质子和α粒子分别在两个完全相同的圆环状空腔中做圆周运动,且在同样的匀强磁场中,比较质子和α粒子在圆环状空腔中运动的动能EH和Eα,运动的周期TH和Tα的大小,有( )
为了科学研究的需要,常常将质子(带有一个正的元电荷,质量为一个原子质量单位)和α粒子(带有两个正的元电荷,质量为四个原子质量单位)等带电粒子贮存在圆环状空腔中,圆环状空腔置于一个与圆环平面垂直的匀强磁场中,带电粒子在其中做匀速圆周运动(如图).如果质子和α粒子分别在两个完全相同的圆环状空腔中做圆周运动,且在同样的匀强磁场中,比较质子和α粒子在圆环状空腔中运动的动能EH和Eα,运动的周期TH和Tα的大小,有( )
 为了科学研究的需要,常常将质子(带有一个正的元电荷,质量为一个原子质量单位)和α粒子(带有两个正的元电荷,质量为四个原子质量单位)等带电粒子贮存在圆环状空腔中,圆环状空腔置于一个与圆环平面垂直的匀强磁场中,带电粒子在其中做匀速圆周运动(如图).如果质子和α粒子分别在两个完全相同的圆环状空腔中做圆周运动,且在同样的匀强磁场中,比较质子和α粒子在圆环状空腔中运动的动能EH和Eα,运动的周期TH和Tα的大小,有( )
为了科学研究的需要,常常将质子(带有一个正的元电荷,质量为一个原子质量单位)和α粒子(带有两个正的元电荷,质量为四个原子质量单位)等带电粒子贮存在圆环状空腔中,圆环状空腔置于一个与圆环平面垂直的匀强磁场中,带电粒子在其中做匀速圆周运动(如图).如果质子和α粒子分别在两个完全相同的圆环状空腔中做圆周运动,且在同样的匀强磁场中,比较质子和α粒子在圆环状空腔中运动的动能EH和Eα,运动的周期TH和Tα的大小,有( )| A. | EH=Eα,TH=Tα | B. | EH≠Eα,TH=Tα | C. | EH=Eα,TH≠Tα | D. | EH≠Eα,TH≠Tα |
5. 质量为m的小球从光滑的半径为R的半圆槽顶部A由静止滑下,已知半圆槽开始时处于静止状态,设槽与桌面无摩擦,则( )
质量为m的小球从光滑的半径为R的半圆槽顶部A由静止滑下,已知半圆槽开始时处于静止状态,设槽与桌面无摩擦,则( )
 质量为m的小球从光滑的半径为R的半圆槽顶部A由静止滑下,已知半圆槽开始时处于静止状态,设槽与桌面无摩擦,则( )
质量为m的小球从光滑的半径为R的半圆槽顶部A由静止滑下,已知半圆槽开始时处于静止状态,设槽与桌面无摩擦,则( )| A. | 小球到达槽底时的动能小于mgR | |
| B. | 小球不可能滑到右边最高点 | |
| C. | 小球升到最大高度时,槽速度为零 | |
| D. | 若球与槽有摩擦,则系统水平方向动量不守恒 |
3.在下列物理过程中,机械能守恒的有( )
| A. | 把一个物体竖直向上匀速提升的过程 | |
| B. | 从地面上发射人造卫星升空的过程 | |
| C. | 汽车关闭油门后沿水平公路向前滑行的过程 | |
| D. | 从高处竖直下落的物体落在竖直的弹簧上,压缩弹簧的过程,对弹簧,物体和地球这一系统 |
2.已知人造航天器在月球表面上空绕月球做匀速圆周运动,经过时间t (t小于航天器的绕行周期),航天器运动的弧长为s,航天器与月球的中心连线扫过角度为θ(θ为弧度制表示),引力常量为G,则( )
| A. | 航天器的轨道半径为$\frac{θ}{S}$ | B. | 航天器的环绕周期为$\frac{4πt}{θ}$ | ||
| C. | 月球的质量为$\frac{{s}^{3}}{Gθ{t}^{2}}$ | D. | 月球的密度为$\frac{3{θ}^{2}}{4G{t}^{2}}$ |
1. 如图所示,一个闭合三角形导线框ABC位于竖直平面内,其下方(略靠前)固定一根与线框平面平行的水平直导线,导线中通以图示方向的恒定电流.释放线框,它由实线位置下落到虚线位置未发生转动,在此过程中( )
如图所示,一个闭合三角形导线框ABC位于竖直平面内,其下方(略靠前)固定一根与线框平面平行的水平直导线,导线中通以图示方向的恒定电流.释放线框,它由实线位置下落到虚线位置未发生转动,在此过程中( )
 如图所示,一个闭合三角形导线框ABC位于竖直平面内,其下方(略靠前)固定一根与线框平面平行的水平直导线,导线中通以图示方向的恒定电流.释放线框,它由实线位置下落到虚线位置未发生转动,在此过程中( )
如图所示,一个闭合三角形导线框ABC位于竖直平面内,其下方(略靠前)固定一根与线框平面平行的水平直导线,导线中通以图示方向的恒定电流.释放线框,它由实线位置下落到虚线位置未发生转动,在此过程中( )| A. | 线框中感应电流方向依次为ACBA→ABCA | |
| B. | 线框所受安培力的合力方向依次为向上→向下→向上 | |
| C. | 线框所受安培力的合力为零,向下做自由落体运动 | |
| D. | 线框的磁通量为零时,感应电流却不为零 |
20.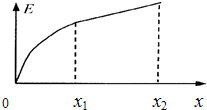 在某集装箱码头上,一架起重机将放在地面上的一个箱子吊起.箱子在起重机钢绳的作用下由静止开始竖直向上运动,运动过程中箱子的机械能E与其位移x关系的图象如图所示,其中0~x1过程的图线为曲线,x1~x2过程的图线为直线.根据图象可知( )
在某集装箱码头上,一架起重机将放在地面上的一个箱子吊起.箱子在起重机钢绳的作用下由静止开始竖直向上运动,运动过程中箱子的机械能E与其位移x关系的图象如图所示,其中0~x1过程的图线为曲线,x1~x2过程的图线为直线.根据图象可知( )
 在某集装箱码头上,一架起重机将放在地面上的一个箱子吊起.箱子在起重机钢绳的作用下由静止开始竖直向上运动,运动过程中箱子的机械能E与其位移x关系的图象如图所示,其中0~x1过程的图线为曲线,x1~x2过程的图线为直线.根据图象可知( )
在某集装箱码头上,一架起重机将放在地面上的一个箱子吊起.箱子在起重机钢绳的作用下由静止开始竖直向上运动,运动过程中箱子的机械能E与其位移x关系的图象如图所示,其中0~x1过程的图线为曲线,x1~x2过程的图线为直线.根据图象可知( )| A. | 0~x1过程中钢绳的拉力逐渐增大 | |
| B. | 0~x1过程中箱子的动能一直增加 | |
| C. | x1~x2过程中钢绳的拉力一直不变 | |
| D. | x1~x2过程中起重机的输出功率一直增大 |
18. 如图,在光滑水平面上有一质量为m1的足够长的木板,其上叠放一质量为m2的木块.假定木块和木板之间的最大静摩擦力和滑动摩擦力相等.现给木块施加一随时间t增大的水平力F=kt(k是常数),木板和木块加速度的大小分别为a1和a2,下列说法中正确的是( )
如图,在光滑水平面上有一质量为m1的足够长的木板,其上叠放一质量为m2的木块.假定木块和木板之间的最大静摩擦力和滑动摩擦力相等.现给木块施加一随时间t增大的水平力F=kt(k是常数),木板和木块加速度的大小分别为a1和a2,下列说法中正确的是( )
 如图,在光滑水平面上有一质量为m1的足够长的木板,其上叠放一质量为m2的木块.假定木块和木板之间的最大静摩擦力和滑动摩擦力相等.现给木块施加一随时间t增大的水平力F=kt(k是常数),木板和木块加速度的大小分别为a1和a2,下列说法中正确的是( )
如图,在光滑水平面上有一质量为m1的足够长的木板,其上叠放一质量为m2的木块.假定木块和木板之间的最大静摩擦力和滑动摩擦力相等.现给木块施加一随时间t增大的水平力F=kt(k是常数),木板和木块加速度的大小分别为a1和a2,下列说法中正确的是( )| A. | 随着时间t增大,始终有a1=a2 | |
| B. | 经过一定时间,木块一定会相对木板相对运动 | |
| C. | 如果木块能相对木板滑动,则之后水平力F的功率随时间均匀增加 | |
| D. | 如果木块能相对木板滑动,则之后摩擦力对木板的功率随时间均匀增加 |
17.闭合线圈在匀强磁场中匀速转动时,产生的正弦式交变电流i=Imsinωt.若保持其他条件不变,使线圈的匝数和转速各增加1倍,则电流的变化规律为( )
0 144221 144229 144235 144239 144245 144247 144251 144257 144259 144265 144271 144275 144277 144281 144287 144289 144295 144299 144301 144305 144307 144311 144313 144315 144316 144317 144319 144320 144321 144323 144325 144329 144331 144335 144337 144341 144347 144349 144355 144359 144361 144365 144371 144377 144379 144385 144389 144391 144397 144401 144407 144415 176998
| A. | i′=Imsinωt | B. | i′=4Imsin 2ωt | C. | i′=2Imsinωt | D. | i′=2Imsin 2ωt |

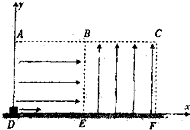 如图所示,绝缘的水平桌面上方有一竖直方向的矩形区域,该区域是由两个边长均为L的正方形区域ABED,BCFE首尾相接组成的,且正方形的下边DE,EF与桌面相接.ABED区域内存在方向水平向右的匀强电场E1,BCFE区域内存在方向竖直向上的匀强电场E2,现有一质量为m,带正电的滑块以$\sqrt{0.5gL}$的初速度从D点水平向右射入场区.已知滑块在两电场中受到的电场力与重力的关系为5F1=F2=5mg,桌面与滑块之间的滑动摩擦因数为μ=0.75,重力加速度为g,滑块可视作质点.
如图所示,绝缘的水平桌面上方有一竖直方向的矩形区域,该区域是由两个边长均为L的正方形区域ABED,BCFE首尾相接组成的,且正方形的下边DE,EF与桌面相接.ABED区域内存在方向水平向右的匀强电场E1,BCFE区域内存在方向竖直向上的匀强电场E2,现有一质量为m,带正电的滑块以$\sqrt{0.5gL}$的初速度从D点水平向右射入场区.已知滑块在两电场中受到的电场力与重力的关系为5F1=F2=5mg,桌面与滑块之间的滑动摩擦因数为μ=0.75,重力加速度为g,滑块可视作质点.