题目内容
 如图1所示,ABCD为倾角为α=37°的矩形斜面,其中AB与底边DC平行,AB=0.6m.BC与AD平行,BC=0.8m.斜面上物体质量2Kg,与斜面的摩擦系数为0.5,在平行斜面方向恒力F的作用下,由静止开始沿斜面对角线从B运动到D.关于F的最小值,给出下面解答:
如图1所示,ABCD为倾角为α=37°的矩形斜面,其中AB与底边DC平行,AB=0.6m.BC与AD平行,BC=0.8m.斜面上物体质量2Kg,与斜面的摩擦系数为0.5,在平行斜面方向恒力F的作用下,由静止开始沿斜面对角线从B运动到D.关于F的最小值,给出下面解答:对物体在面ABCD上作受力分析,有三个力,恒力F、重力沿斜面向下的分力GX、摩擦力f(如图2),经判断恒力F与AB边平行时最小,且可以用F=
f2+
|
分析:若恒力F与AB边平行时最小,由平行四边形定则求出F的值.由于GX沿BD方向的力大于摩擦力,F在平行斜面时与BD垂直最小,求出F的最小值.分析物体的运动情况,由动能定理求解做木块到达D点时的动能大小.
解答:解:“经判断恒力F与AB边平行时最小,且可以用F=
进行计算”.这个分析是错误的,将重力分解为沿斜面和垂直于斜面两个方向,斜面方向的分力为Gx.
GX=mgsinα=12N,GX沿BD方向的力为Gxcos37°=9.6N,
摩擦力f=μmgcosα=8N,则Gxcos37°大于摩擦力,所以物体作加速运动,合力不为零,所以不能用F=
进行计算F.
所以F在平行斜面时与BD垂直即为最小,F最小=GXsin37°=7.2N.
物体运动到斜面底端时动能的计算,由动能定理:Ek=mgh-fs
其中 h=BC×Sinα,s=
=1m
所以,Ek=2×10×0.8×0.6-8×1J=1.6J
答:用F=
计算F是错误的,因为物体作加速运动,合力不为零,木块到达D点时的动能大小为1.6J.
f2+
|
GX=mgsinα=12N,GX沿BD方向的力为Gxcos37°=9.6N,
摩擦力f=μmgcosα=8N,则Gxcos37°大于摩擦力,所以物体作加速运动,合力不为零,所以不能用F=
f2+
|
所以F在平行斜面时与BD垂直即为最小,F最小=GXsin37°=7.2N.
物体运动到斜面底端时动能的计算,由动能定理:Ek=mgh-fs
其中 h=BC×Sinα,s=
| (AB)2+(BC)2 |
所以,Ek=2×10×0.8×0.6-8×1J=1.6J
答:用F=
| f2+G2 |
点评:本题关键通过分析重力,在斜面平面内研究物体的受力情况,判断其运动情况.再根据动能定理求解木块到达D点时的动能大小

练习册系列答案
相关题目
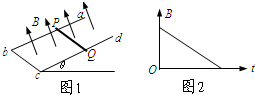 如图1所示,abcd是由导体做成的框架,其平面与水平面成θ角,质量为m的导体棒PQ与光滑导轨ab、cd接触良好,回路面积为S.整个装置放在垂直于框架平面的磁场中,磁感应强度随时间变化情况如图2所示,PQ始终静止.则下面说法正确的是( )
如图1所示,abcd是由导体做成的框架,其平面与水平面成θ角,质量为m的导体棒PQ与光滑导轨ab、cd接触良好,回路面积为S.整个装置放在垂直于框架平面的磁场中,磁感应强度随时间变化情况如图2所示,PQ始终静止.则下面说法正确的是( )| A、导体棒PQ所受安培力的大小为mgsinθ | B、导体棒PQ所受安培力的方向水平向右 | C、回路中感应电动势的大小为△B/△t | D、导体棒中感应电流的方向由P到Q |
 如图1所示,abcd是位于竖直平面内的正方形闭合金属线框,其质量为m,电阻为R.在金属线框的下方有一匀强磁场区域,PQ和P?Q?是该匀强磁场区域的水平边界,并与线框的bc边平行,磁场方向与线框平面垂直.现金属线框由距PQ某一高度处从静止开始下落,经时间t0后刚好到达PQ边缘,速度为v0,假设线框所受的空气阻力恒定.图2是金属线框由静止开始下落到完全穿过匀强磁场区域过程中的速度-时间图象.
如图1所示,abcd是位于竖直平面内的正方形闭合金属线框,其质量为m,电阻为R.在金属线框的下方有一匀强磁场区域,PQ和P?Q?是该匀强磁场区域的水平边界,并与线框的bc边平行,磁场方向与线框平面垂直.现金属线框由距PQ某一高度处从静止开始下落,经时间t0后刚好到达PQ边缘,速度为v0,假设线框所受的空气阻力恒定.图2是金属线框由静止开始下落到完全穿过匀强磁场区域过程中的速度-时间图象. 后刚好到达PQ边缘,速度为
后刚好到达PQ边缘,速度为 ,假设线框所受的空气阻力恒定。图2是金属线框由静止开始下落到完全穿过匀强磁场区域过程中的速度—时间图象。
,假设线框所受的空气阻力恒定。图2是金属线框由静止开始下落到完全穿过匀强磁场区域过程中的速度—时间图象。
