题目内容
(21分)如图所示,将一端带有半圆形光滑轨道的凹槽固定在水平面上,凹槽的水平部分AB粗糙且与半圆轨道平滑连接,AB长为2L。圆轨道半径为![]() 。凹槽的右端固定一原长为L的轻质弹簧P1,P1的左端与长为L质量为2m的圆筒相接触,但不栓接。圆筒内部右端栓接一完全相同的弹簧P2,用直径略小于圆筒内径、质量为m的小球将弹簧P2压缩
。凹槽的右端固定一原长为L的轻质弹簧P1,P1的左端与长为L质量为2m的圆筒相接触,但不栓接。圆筒内部右端栓接一完全相同的弹簧P2,用直径略小于圆筒内径、质量为m的小球将弹簧P2压缩![]() ,再用销钉K将小球锁定在圆筒内(小球与P2不栓接)。球与圆筒内壁间的动摩擦因数为u,圆筒与凹槽水平部分间的动摩擦因数为2u。用圆筒将弹簧P1也压缩
,再用销钉K将小球锁定在圆筒内(小球与P2不栓接)。球与圆筒内壁间的动摩擦因数为u,圆筒与凹槽水平部分间的动摩擦因数为2u。用圆筒将弹簧P1也压缩![]() •,由静止释放,圆筒恰好不滑动。现将销钉K突然拔掉,同时对圆筒施加一水平向左的拉力,使圆筒向左做匀加速运动,到B点时圆筒被卡住立刻停止运动,小球沿半圆形轨道从C点水平抛出。设最大静摩擦力等于滑动摩擦力,重力加速度为g,小球可视为质点,圆筒壁的厚度忽略不计。
•,由静止释放,圆筒恰好不滑动。现将销钉K突然拔掉,同时对圆筒施加一水平向左的拉力,使圆筒向左做匀加速运动,到B点时圆筒被卡住立刻停止运动,小球沿半圆形轨道从C点水平抛出。设最大静摩擦力等于滑动摩擦力,重力加速度为g,小球可视为质点,圆筒壁的厚度忽略不计。
(1) 若小球通过半圆形轨道最高点C时,轨道对小球的压力是小球重力的3倍,求小球射出圆筒时的速度大小
(2) 若使圆筒运动到B点之前,弹簧P2长度不变,求拉力初始值的取值范围
(3) 若拉力的初始值为![]() ,且小球从C处平拋后,恰好未撞击圆筒,求圆筒从静止运动到B点过程中拉力所做的功
,且小球从C处平拋后,恰好未撞击圆筒,求圆筒从静止运动到B点过程中拉力所做的功

(21分)解:
(1)(6分)小球过最高点时,根据向心力公式 ![]()
![]() ………….2分
………….2分
小球从B点到最高点C过程中机械能守恒 ![]() …………….2分
…………….2分
![]() …………………………….2分
…………………………….2分
(2)(10分)由于筒恰好不动,对筒和小球: ![]() ……………………2分
……………………2分
拔掉销钉,设小球所允许的加速度最大值是![]() ,应有
,应有
![]() ………………………2分
………………………2分
最小值是![]() ,应有
,应有 ![]() ………………………2分
………………………2分
刚拔掉销钉时,对筒和小球: ![]() …………………2分
…………………2分
且![]()
以上解得: 15umg≤F≤21umg ……………………………2分
(3)(5分)
拉力的初始值为![]() ,所以给定初始拉力仍在上问范围内,在运动到B点以前,弹簧P2的长度不变,设加速度为a0,对整体:
,所以给定初始拉力仍在上问范围内,在运动到B点以前,弹簧P2的长度不变,设加速度为a0,对整体:
18umg+kL/2-2u×3mg=3ma 0 …………………………1分
到B处时,VB2=2a0L/2
从C点平抛 L=VCt L/2=1/2gt2
从开始到小球运动到C点,对小球:
W2-umgL/2-mgL/2=mVc2/2 – mVB2/2
对筒和小球整体,从静止开始运动到B点,由功能关系得
WF+W1-2u×3mg×L/2=3mVB2/2 ……………1分
而两弹簧相同,形变量相同,所以有W1=W2
联立以上解之得
…………………………1分

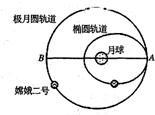 2010年 10 月 26 日 21时 27 分,北京航天飞行控制中心对“嫦娥二号”卫星实施了降轨控制,卫星成功由轨道半径为 a、周期为 Tl 的极月圆轨道进入远月点距离为 a、周期为T2的椭圆轨道,为在月球虹湾区拍摄图象做好准备,轨道如图所示.则“嫦娥二号”( )
2010年 10 月 26 日 21时 27 分,北京航天飞行控制中心对“嫦娥二号”卫星实施了降轨控制,卫星成功由轨道半径为 a、周期为 Tl 的极月圆轨道进入远月点距离为 a、周期为T2的椭圆轨道,为在月球虹湾区拍摄图象做好准备,轨道如图所示.则“嫦娥二号”( )| A、在圆轨道运行周期T1小于它在椭圆轨道运行周期T2 | B、经过圆轨道上B点时的速率大于它经过椭圆轨道上A点时的速率 | C、在圆轨道上经过B点和在椭圆轨道上经过A点时的加速度大小相等 | D、在圆轨道上经过B点和在椭圆轨道上经过A点时的机械能相等 |
 2011年9月29日晚21时16分,我国将首个目标飞行器天宫一号发射升空,它将在两年内分别与神舟八号、神舟九号、神舟十号飞船对接,从而建立我国第一个空间实验室.假如神舟八号与天宫一号对接前所处的轨道如图所示.下列说法正确的是( )
2011年9月29日晚21时16分,我国将首个目标飞行器天宫一号发射升空,它将在两年内分别与神舟八号、神舟九号、神舟十号飞船对接,从而建立我国第一个空间实验室.假如神舟八号与天宫一号对接前所处的轨道如图所示.下列说法正确的是( )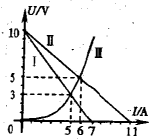 (1)如图所示,直线I、Ⅱ分别是电源1与电源2的路端电压随输出电流变化的图线,曲线Ⅲ是一个小灯泡的伏安特性曲线,则电源1和电源2的内阻之比为
(1)如图所示,直线I、Ⅱ分别是电源1与电源2的路端电压随输出电流变化的图线,曲线Ⅲ是一个小灯泡的伏安特性曲线,则电源1和电源2的内阻之比为
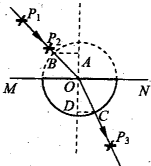 示,某同学用插针法测定一半圆形玻璃砖的折射率,在平铺的白纸上垂直纸面插大头针P1、P2确定入射光线,
示,某同学用插针法测定一半圆形玻璃砖的折射率,在平铺的白纸上垂直纸面插大头针P1、P2确定入射光线,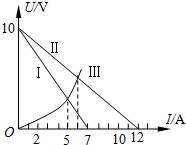 如图所示,直线Ⅰ、Ⅱ分别是电源Ⅰ与电源Ⅱ的路端电压随输出电流变化的特性曲线,曲线Ⅲ是一个小灯泡的伏安特性曲线,则( )
如图所示,直线Ⅰ、Ⅱ分别是电源Ⅰ与电源Ⅱ的路端电压随输出电流变化的特性曲线,曲线Ⅲ是一个小灯泡的伏安特性曲线,则( )