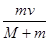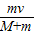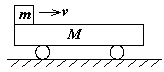题目内容
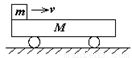
 M置于光滑平面上,上表面粗糙且足够长,木块m以初速度v滑上车表面,则( )
M置于光滑平面上,上表面粗糙且足够长,木块m以初速度v滑上车表面,则( )分析:以小车和木块组成的系统为研究对象所受合外力为零,因此系统动量守恒,根据动量守恒列方程即可解答.
相对运动过程中系统机械能减小,转化为摩擦产生的内能.
相对运动过程中系统机械能减小,转化为摩擦产生的内能.
解答:解:A、以小车和木块组成的系统为研究对象所受合外力为零,因此系统动量守恒,
由于摩擦力的作用,m速度减小,M速度增大,m速度减小到最小时,M速度达最大,最后m、M以共同速度运动.
mv=(m+M)v′
v′=
相对运动过程中系统机械能减小,转化为摩擦产生的内能,根据能量守恒得:
E损=
mv2-
(m+M)v′2
故A正确,D错误.
B、车表面粗糙,小车与木块间的力属于内力,不是判断系统动量是否守恒的条件.故B错误.
C、根据A选项分析,小车M获得动量Mv′与车面粗糙程度无关,故C错误.
故选A.
由于摩擦力的作用,m速度减小,M速度增大,m速度减小到最小时,M速度达最大,最后m、M以共同速度运动.
mv=(m+M)v′
v′=
| mv |
| M+m |
相对运动过程中系统机械能减小,转化为摩擦产生的内能,根据能量守恒得:
E损=
| 1 |
| 2 |
| 1 |
| 2 |
故A正确,D错误.
B、车表面粗糙,小车与木块间的力属于内力,不是判断系统动量是否守恒的条件.故B错误.
C、根据A选项分析,小车M获得动量Mv′与车面粗糙程度无关,故C错误.
故选A.
点评:应用动量守恒定律时要清楚研究的对象和守恒条件.
把动量守恒和能量守恒结合起来列出等式求解是常见的问题.
把动量守恒和能量守恒结合起来列出等式求解是常见的问题.

练习册系列答案
相关题目
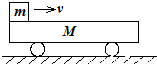
M置于光滑平面上,上表面粗糙且足够长,木块m以初速度v滑上车表面,则( )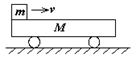
A.m的最终速度为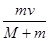 |
| B.因车表面粗糙,故系统动量不守恒 |
| C.车面越粗糙,小车M获得动量越大 |
| D.车面越粗糙,系统产生的内能越多 |