题目内容
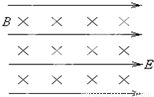
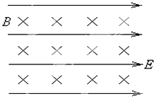 在空间有一水平方向的匀强电场,场强E=10
在空间有一水平方向的匀强电场,场强E=10| 3 |
分析:粒子开始受重力、电场力和洛伦兹力平衡,做匀速直线运动,根据共点力平衡求出粒子运动的速度大小和速度与电场线方向的夹角.撤去磁场,粒子受重力和电场力做曲线运动,将曲线运动分解为沿电场方向和垂直于电场方向,根据受力确定粒子在两个方向上的运动情况,结合牛顿第二定律和运动学公式进行求解.
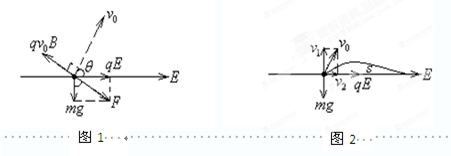
解答:解:由题意,在撤去磁场前,粒子受力情况如图1所示.
由力的平衡,有(qv0B)2=(mg)2+(qE)2
tanθ=
解得 v0=2m/s θ=60°
撤去磁场后,如图2所示,v1=v0sinθ=
m/s
v2=v0cosθ=1m/s
粒子在竖直方向做竖直上抛运动,返回“抛出点”所用时间t=
=
=
s
粒子在水平方向做匀加速直线运动,加速度a2=
=10
m/s2
在时间t内的位移s=v2t+
a2t2=
m≈1.4m.
答:沿电场线方向上移动了1.4m.
由力的平衡,有(qv0B)2=(mg)2+(qE)2
tanθ=
| qE |
| mg |
解得 v0=2m/s θ=60°
撤去磁场后,如图2所示,v1=v0sinθ=
| 3 |
v2=v0cosθ=1m/s
粒子在竖直方向做竖直上抛运动,返回“抛出点”所用时间t=
| 2v1 |
| a1 |
| 2v1 |
| g |
| ||
| 5 |
粒子在水平方向做匀加速直线运动,加速度a2=
| qE |
| M |
| 3 |
在时间t内的位移s=v2t+
| 1 |
| 2 |
| 4 |
| 5 |
| 3 |

答:沿电场线方向上移动了1.4m.
点评:本题考查了粒子在复合场中运动,关键理清粒子的运动情况,结合牛顿第二定律和运动学公式进行求解.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
 如图所示,空间有一水平方向的匀强电场,初速度为v0的带电小球从A点射入电场,在竖直平面内沿直线从A运动到B,在此过程中粒子的( )
如图所示,空间有一水平方向的匀强电场,初速度为v0的带电小球从A点射入电场,在竖直平面内沿直线从A运动到B,在此过程中粒子的( )| A、动能和电势能之和减少,重力势能增加 | B、动能增加,重力势能和电势能之和减小 | C、动能和重力势能之和增加,电势能减少 | D、动能不变,重力势能增加,电势能减少 |
 如图所示,空间有一水平方向的匀强电场,初速度为v0的带电小球从A点射入电场,在竖直平面内沿直线从A运动到B,在此过程中粒子的( )
如图所示,空间有一水平方向的匀强电场,初速度为v0的带电小球从A点射入电场,在竖直平面内沿直线从A运动到B,在此过程中粒子的( )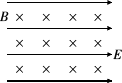
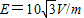 ,又有一与电场方向垂直的匀强磁场,磁感应强度B=10T,如图所示.现有一个质量m=2×10-6kg,电量q=2×10-6C的带正电的粒子在这个电磁场区域中的竖直平面内做匀速直线运动.假如在这个带电粒子经过某条电场线时突然撤去磁场,那么,当它再次经过同一条电场线时,沿电场线方向上移动了多大的距离S(g取10m/s2).
,又有一与电场方向垂直的匀强磁场,磁感应强度B=10T,如图所示.现有一个质量m=2×10-6kg,电量q=2×10-6C的带正电的粒子在这个电磁场区域中的竖直平面内做匀速直线运动.假如在这个带电粒子经过某条电场线时突然撤去磁场,那么,当它再次经过同一条电场线时,沿电场线方向上移动了多大的距离S(g取10m/s2).