题目内容
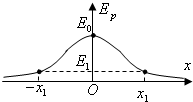（2013?扬州模拟）空间存在一电场，一带负电的粒子仅在电场力作用下从x1处沿x轴负方向运动，初速度大小为v0，其电势能Ep随坐标x变化的关系如图所示，图线关于纵轴左右对称，以无穷远处为零电势能点，粒子在原点O处电势能为E0，在x1处电势能为E1，则下列说法中不正确的是（ ）分析：根据电势能与电势的关系：Ep=qφ，场强与电势的关系：E=
，结合分析图象斜率与场强的关系，即可求得原点O处的电场强度；速度根据能量守恒判断；
根据斜率读出场强的变化，由F=qE，分析电场力的变化，由牛顿第二定律判断加速度的变化．
| △φ |
| △x |
根据斜率读出场强的变化，由F=qE，分析电场力的变化，由牛顿第二定律判断加速度的变化．
解答：解：A、根据电势能与电势的关系：Ep=qφ，场强与电势的关系：E=
，得：E=
?
．Ep-x图象切线的斜率等于
，根据数学知识可知，坐标原点O处切线斜率为零，则坐标原点O处电场强度为零，故A正确．
B、由图看出，x1、-x1两处的电势能相等，根据能量守恒定律得知，粒子经过x1、-x1处速度相同，故B正确．
C、由x1运动到O过程，根据数学知识可知，图线的斜率先减小后增大，说明场强先减小后增大，由F=qE知，粒子所受的电场力先减小后增大，根据牛顿第二定律得知，加速度先减小后增大，故C错误．
D、根据公式Ep=qφ，可知，该粒子带负电，从x1处到-x1处，电势先降低后升高，电场方向先沿x轴负方向后沿x轴正方向，电场力先沿x轴正方向后沿x轴负方向，粒子只要能通过原点O，就能一直沿x轴运动，设粒子恰好能到达原点O时的速度为v，则根据能量守恒定律得：
mv2=E0-E1，v=
，当v0＞v时，即v0＞
粒子能够一直沿x轴负方向运动，故D正确．
本题选错误的，故选：C
| △φ |
| △x |
| 1 |
| q |
| △Ep |
| △x |
| △Ep |
| △x |
B、由图看出，x1、-x1两处的电势能相等，根据能量守恒定律得知，粒子经过x1、-x1处速度相同，故B正确．
C、由x1运动到O过程，根据数学知识可知，图线的斜率先减小后增大，说明场强先减小后增大，由F=qE知，粒子所受的电场力先减小后增大，根据牛顿第二定律得知，加速度先减小后增大，故C错误．
D、根据公式Ep=qφ，可知，该粒子带负电，从x1处到-x1处，电势先降低后升高，电场方向先沿x轴负方向后沿x轴正方向，电场力先沿x轴正方向后沿x轴负方向，粒子只要能通过原点O，就能一直沿x轴运动，设粒子恰好能到达原点O时的速度为v，则根据能量守恒定律得：
| 1 |
| 2 |
|
|
本题选错误的，故选：C
点评：解决本题的关键要分析图象斜率的物理意义，判断电势和场强的变化，再根据力学基本规律：牛顿第二定律和能量守恒定律进行分析．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
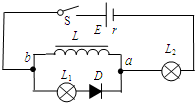（2013?扬州模拟）如图所示，电源的电动势为E、内阻为r，L1、L2为两个相同的灯泡，线圈L的直流电阻不计，与灯泡L1连接的是一只理想二极管D．下列说法中正确的是（ ）
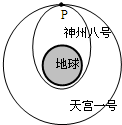（2013?扬州模拟）我国发射的“神舟八号”飞船与先期发射的“天宫一号”空间站实现了完美对接．已知“天宫一号”绕地球做圆轨道运动，假设沿椭圆轨道运动的“神州八号”环绕地球的运动方向与“天宫一号”相同，远地点与“天宫一号”的圆轨道相切于某点P，并在该点附近实现对接，如图所示．则下列说法正确的是（ ）
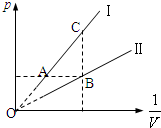（2013?扬州模拟）某同学用同一注射器封闭了一定质量的理想气体在早晨和中午分别做了“验证玻意耳定律”的实验，中午气温高于早晨，他将实验结果绘成如图所示的
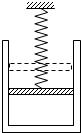（2013?扬州模拟）如图所示，在一个质量为M、横截面积为S的圆柱形导热气缸中，用活塞封闭了一部分空气，气体的体积为V0，活塞与气缸壁间密封且光滑，一弹簧秤连接在活塞上，将整个气缸悬吊在天花板上．当外界气温升高（大气压保持为p0）时，则弹簧秤的示数