题目内容
如图所示，AO、BO、CO为三根轻绳，OB与水平天花板夹角为60°，物体质量m=2Kg．求AO、BO绳所受拉力．
分析：分析结点O的受力情况，受到CO绳的拉力、AO绳的拉力和BO绳的拉力处于平衡，其中CO绳的拉力大小等于物体的重力G，根据共点力平衡，运用正交分解求出两个拉力的大小．
解答：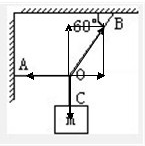
解：以结点O为研究对象，分析受力情况如图，受到CO绳的拉力、AO绳的拉力和BO绳的拉力，平衡时，FC=mg=20N
根据平衡条件得
TOBsin60°=mg
TOBcos60°=TOA
解得：TOA=
N
TOB=
N
答：AO、BO绳所受拉力分别为
N、
N．
解：以结点O为研究对象，分析受力情况如图，受到CO绳的拉力、AO绳的拉力和BO绳的拉力，平衡时，FC=mg=20N根据平衡条件得
TOBsin60°=mg
TOBcos60°=TOA
解得：TOA=
20
| ||
| 3 |
TOB=
40
| ||
| 3 |
答：AO、BO绳所受拉力分别为
20
| ||
| 3 |
40
| ||
| 3 |
点评：解决本题的关键正确地进行受力分析，运用正交分解进行求解．
练习册系列答案
相关题目
如图所示，AO和BO悬挂一个重物，现将绳子AO由如图所示的位置移到竖直，该过程中，OB绳子始终保持水平，则下列说法中正确的是（ ）
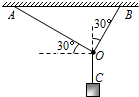如图所示，AO、BO、CO三根轻绳系于同一点O，A、B固定在水平天花板上，C处挂一质量为m的物体，AO与水平方向成30°角，BO与竖直方向成30°角．若轻绳AO、BO、CO对O点的拉力分别为TA、TB、TC，则（ ）
如图所示，AO、BO两轻绳悬挂一重为200N的物体，求AO绳、BO绳对重物拉力大小各为多大？若AO、BO两轻绳能承受的最大拉力均为T=200