题目内容
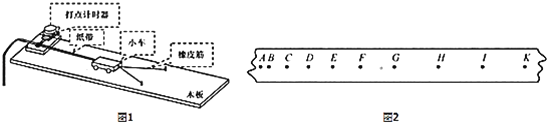
【题目】如图所示,劲度系数k=25N/m轻质弹簧的一端与竖直板P拴接(竖直板P固定在木板B的左端),另一端与质量mA=1kg的小物体A相连,P和B的质量为MB=4kg且B足够长.A静止在木板B上,A右端连一细线绕过光滑的定滑轮与质量mC=1kg的物体C相连.木板B的上表面光滑,下表面与地面的动摩擦因数μ=0.4.开始时用手托住C,让细线恰好伸直但没拉力,然后由静止释放C,直到B开始运动.已知弹簧伸长量为x时其弹性势能为![]() .全过程物体C没有触地,弹簧在弹性限度内,g取10m/s2.求:
.全过程物体C没有触地,弹簧在弹性限度内,g取10m/s2.求:

(1)释放C瞬间A的加速度大小;
(2)释放C后A的最大速度大小;
(3)若C的质量变为m/C=3kg,则B刚开始运动时,拉力对物体A做功的功率.
【答案】(1)5m/s2 (2) ![]() m/s (3)45
m/s (3)45![]() W
W
【解析】
(1)对物体C:mCg-FT=mCa
对物体A:FT=mAa
所以a=![]() =5m/s2
=5m/s2
(2)水平面对B的摩擦力Ff=μFN=μ(mA+MB)g=20N,释放C后B不会运动.
所以,当A的加速度为0时其速度最大,有kx=mCg,x=0.4m
对物体A、C用动能定理mCgx+W=![]()
W=Fl=-![]() ·x=-
·x=-![]() ,
,
联立解得:vm=![]() m/s
m/s
(3)设B刚开始运动时弹簧伸长量为x1,弹力F=kx1,当F=Ff时木板B开始运动,
则kx1=μ(mA+MB)g,x1=0.8m
弹簧弹力对物体A所做的功W1=-![]() ,
,
若B刚开始运动时A的速度为v,
对物体A、C用动能定理![]()
v=2![]() m/s
m/s
设B刚要运动时细线的拉力为FT1
对物体C:mC′g-FT1=mC′a′,对物体A:FT1-kx1=mAa′,
FT1=![]() =22.5N,功率P=FT1v=45
=22.5N,功率P=FT1v=45![]() W。
W。

 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案【题目】(6分)某物理小组的同学设计了一个粗制玩具小车通过凹形桥最低点时的速度的实验。所用器材有:玩具小车、压力式托盘秤、凹形桥模拟器(圆弧部分的半径为R=0.20m)。
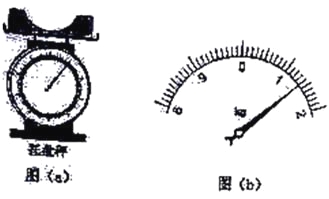
完成下列填空:
(1)将凹形桥模拟器静置于托盘秤上,如图(a)所示,托盘秤的示数为1.00kg;
(2)将玩具小车静置于凹形桥模拟器最低点时,托盘秤的示数如图(b)所示,该示数为_____kg;
(3)将小车从凹形桥模拟器某一位置释放,小车经过最低点后滑向另一侧,此过程中托盘秤的最大示数为m;多次从同一位置释放小车,记录各次的m值如下表所示:
序号 | 1 | 2 | 3 | 4 | 5 |
m(kg) | 1.80 | 1.75 | 1.85 | 1.75 | 1.90 |
(4)根据以上数据,可求出小车经过凹形桥最低点时对桥的压力为_____N;小车通过最低点时的速度大小为_______m/s。(重力加速度大小取9.80m/s2 ,计算结果保留2位有效数字)