题目内容
如图，水平面上O点右侧空间有一匀强电场，场强大小E=6×106N/C，方向水平向右，在O处放一个质量为m=0.1kg、带电量q=-5×10-8C的绝缘物块，它与水平面之间的动摩擦因数μ=0.2．现给物块一个水平向右的初速度v0=2m/s，（已知物块与水平面间的最大静摩擦力等于其滑动摩擦力，g取10m/s2）求：（1）物块第一次速度为零时，该点与O点电势差的大小；
（2）物块最终停止时，该点与O点的水平距离．
分析：物块先向右做匀减速直线运动到零，然后返回做匀加速直线运动，离开电场后再做匀减速运动直到停止．由动能定理求出物块最终静止时距O点的距离
解答：解：（1）设物块向右水平运动，在A点第一次速度为零时，距O点距离为x1
由题中数据得：F电=Eq=0.3N； Ff=μmg=0.2N
由动能定理：（F电+Ff）x1=
mv2，得x1=0.4m
该点与O点电势差的大小
U=Ex1
=6×106×0.4=2.4×106V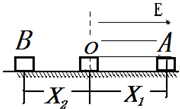
（2）在A点，由于F电＞Ff，物块会反向运动，最终在O点左侧
无电场场区域静止，设该点为B点，与O点距离为x2
由动能定理：：F电x1-Ff（x1+x2）=0
得 x2=0.2m
答：（1）物块第一次速度为零时，该点与O点电势差的大小2.4×106V；
（2）物块最终停止时，该点与O点的水平距离0.2m处．
由题中数据得：F电=Eq=0.3N； Ff=μmg=0.2N
由动能定理：（F电+Ff）x1=
| 1 |
| 2 |
该点与O点电势差的大小
U=Ex1
=6×106×0.4=2.4×106V
（2）在A点，由于F电＞Ff，物块会反向运动，最终在O点左侧
无电场场区域静止，设该点为B点，与O点距离为x2
由动能定理：：F电x1-Ff（x1+x2）=0
得 x2=0.2m
答：（1）物块第一次速度为零时，该点与O点电势差的大小2.4×106V；
（2）物块最终停止时，该点与O点的水平距离0.2m处．
点评：本题首先要理清物块的运动过程，运用动能定理即可正确解题．
练习册系列答案
相关题目
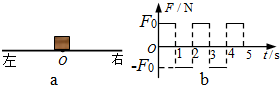
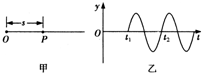选做题：请从A、B和C三小题中选定两小题作答，并在答题卡上把所选题目对应字母后的方框涂满涂黑．如都作答，则按A、B两小题评分．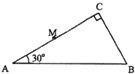
，方向水平向右，在O处放一个质量为m=0.1kg、带电量
的绝缘物块，它与水平面之间的动摩擦因数μ=0.2。现给物块一个水平向右的初速度
，(已知物块与水平面间的最大静摩擦力等于其滑动摩擦力，g取10m/s2)求:
，方向水平向右，在O处放一个质量为m=0.1kg、带电量
的绝缘物块，它与水平面之间的动摩擦因数μ=0.2。现给物块一个水平向右的初速度
，(已知物块与水平面间的最大静摩擦力等于其滑动摩擦力，g取10m/s2)求: