题目内容

A和B是绕地球做匀速圆周运动的卫星，mA=2mB，轨道半径RA=2RB，则B与A的（　　）
分析：人造地球卫星绕地球做匀速圆周运动时，万有引力提供向心力，据G
Mm
R2
=ma=
mv2
R
=mω2R=m
4π2
T2
R，由题设给定条件分析可得
解答：解：A、根据公式：G
Mm
R2
=ma，得：
aA
aB
=
R
2
B
R
2
A
=
1
4
．故A正确；
B、根据公式：G
Mm
R2
=m
4π2
T2
R得：T=2π
R3
GM
，所以：
TB
TA
=
R
3
B
R
3
A
=
1
8
=
1
2
2
．故B错误；
C、根据公式：G
Mm
R2
=
mv2
R
得：v=
GM
R
，所以：
vB
vA
=
RA
RB
=
2
1
．故C错误；
D、根据公式：G
Mm
R2
=mω2R得：ω=
GM
R3
，所以：
ωB
ωA
=
R
3
A
R
3
B
=
8
1
=
2
2
1
．故D错误．
故选：A
点评：熟练掌握万有引力提供卫星圆周运动的向心力，并能写出向心力的不同表达式．
练习册系列答案
相关题目
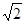A和B是绕地球做匀速圆周运动的卫星，mA=mB，轨道半径RB=2RA，则A与B的（　　）
A 和B是绕地球做匀速圆周运动的卫星，已知mA=2mB，轨道半径RA=
1
2
RB，则B与A的（　　）
A和B是绕地球做匀速圆周运动的卫星，mA=2mB，轨道半径RB=2RA，则B与A的（    ）

A.加速度之比为4∶1

B.周期之比为∶1

C.线速度之比为1∶

D.角速度之比为1∶

43、A和B是绕地球做匀速圆周运动的卫星，mA=mB,轨道半径RB=2RA，则A与B的：

A．加速度之比为4∶1             B．周期之比为2∶1

 C．线速度之比为1∶          D．角速度之比为∶1

 

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网