题目内容
【题目】如图(a)所示,在倾角![]() 的光滑固定斜面上有一劲度系数k=100N/m的轻质弹簧,弹簧下端固定在垂直于斜面的挡板上,弹簧上端拴接一质量m=2 kg的物体,初始时物体处于静止状态。取g=10 m/s2。
的光滑固定斜面上有一劲度系数k=100N/m的轻质弹簧,弹簧下端固定在垂直于斜面的挡板上,弹簧上端拴接一质量m=2 kg的物体,初始时物体处于静止状态。取g=10 m/s2。
(1)求此时弹簧的形变量x0;
(2)现对物体施加沿斜面向上的拉力F,拉力F的大小与物体位移x的关系如图(b)所示,设斜面足够长。
a.分析说明物体的运动性质并求出物体的速度v与位移x的关系式;
b.若物体位移为0.1m时撤去拉力F,在图(c)中做出此后物体上滑过程中弹簧弹力f的大小随形变量![]() 的函数图像;并且求出此后物体沿斜面上滑的最大距离xm以及此后运动的最大速度vm。
的函数图像;并且求出此后物体沿斜面上滑的最大距离xm以及此后运动的最大速度vm。
【答案】(1)x0=0.1 m;(2)0.99m/s
【解析】试题分析:(1)初始状态时物体处于平衡状态,则有:kx0=mgsinθ
代入数据解得x0=0.1m;
(2)a.设物体运动微小位移x的过程中加速度为a,根据牛顿第二定律有:
F+k(x0-x)-mgsinθ=ma
根据F-x图象可知,F=4.8+100x
联立解得:a=2.4m/s2;
弹簧发生拉伸形变时,上述结论仍成.可见,物体做加速度a=2.4m/s2的加速直线运动.
根据运动学公式可和物体的速度大小v随x变化的表达式为:v2=2ax
代入数据解得:v2=4.8x
b.物体位移x=0.1m后撤去拉力,此后物体上滑过程中弹力f随形变量x′的图象如下图所示;
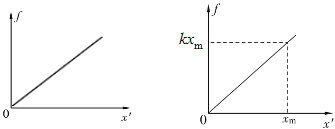
物体上滑过程中克服弹力所做的功对应右上图中的面积,即Wf=![]() kxm2
kxm2
撤去拉力后,在上滑过程中根据动能定理有:-mgxmsinθ-Wf=0-![]() mv2
mv2
联立以上可得,xm=0.04m;
物体再次回到初始位置时速度最大,对于全过程只有拉力F对物体做功
拉力F对图象做的功为F-x图象下的面积,则有: ![]() ;
;
根据动能定理可得:WF=![]() mvm2
mvm2
联立解得:vm=0.7![]() m/s=0.99m/s;
m/s=0.99m/s;