题目内容
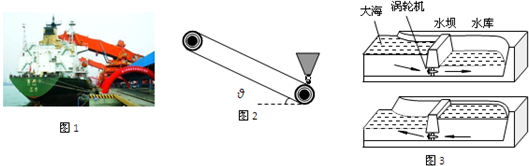
 如图所示,传送带与水平面之间的夹角为θ=30°,其上A、B两点间的距离为L=5m,传送带在电动机的带动下以v=1m/s的速度匀速运动,现将一质量为m=10kg的小物体(可视为质点)轻放在传送带的A点,已知小物体与传送带之间的动摩擦因数μ=
如图所示,传送带与水平面之间的夹角为θ=30°,其上A、B两点间的距离为L=5m,传送带在电动机的带动下以v=1m/s的速度匀速运动,现将一质量为m=10kg的小物体(可视为质点)轻放在传送带的A点,已知小物体与传送带之间的动摩擦因数μ=
| ||
| 2 |
(1)传送带对小物体做的功;
(2)电动机做的功.
分析:(1)由牛顿第二定律可求得物体运动的加速度;而物体和传送带速度相等时二者相对静止,由位移公式可求得物体加速上滑的位移;则由动能定理即可求得摩擦力对物体所做的功;
(2)电动机所做的功转化为物体增加的机械能系统增加的内能;由功能关系可求得电动机所做的功.
(2)电动机所做的功转化为物体增加的机械能系统增加的内能;由功能关系可求得电动机所做的功.
解答:解:(1)物体刚放上A点时,受到的滑动摩擦力沿传送带向上,物体作匀加速直线运动,此时:a=
=g(μcosθ-sinθ)=10×(
×
-
)=2.5m/s2
假设物体能与皮带达到相同的速度,则物体加速上滑的位移为x1=
=
=0.2m<L=5m
假设成立,物体加速完达到v=1m/s后,将匀速向上运动,到达B点时速度仍为v=1m/s,所以:
从A到B,由动能定理:
mv2-0=W传-mgLsinθ,
代入数据,解得:W传=255J
或者:传送带对物体做的功,其实也就是摩擦力对物体做的功,
物体匀速向上运动的位移为:x2=L-x1=4.8m(1分)W传=μmgcosθ?x1+mgsinθ?x2=255J
(2)由功能关系可知,电动机做的功等于物块增加的机械能和因滑动摩擦而发的热,所以:
相对滑动时:S相=v?
-x1=0.2m
所以,由功能关系得:W电=(mgLsinθ+
mv2)+μmgcosθ?S相=270J;
答:(1)传送带对物体所做的功为255J;(2)电动机所做的功为270J.
| μmgcosθ-mgsinθ |
| m |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
假设物体能与皮带达到相同的速度,则物体加速上滑的位移为x1=
| v2 |
| 2a |
| 12 |
| 2×2.5 |
假设成立,物体加速完达到v=1m/s后,将匀速向上运动,到达B点时速度仍为v=1m/s,所以:
从A到B,由动能定理:
| 1 |
| 2 |
代入数据,解得:W传=255J
或者:传送带对物体做的功,其实也就是摩擦力对物体做的功,
物体匀速向上运动的位移为:x2=L-x1=4.8m(1分)W传=μmgcosθ?x1+mgsinθ?x2=255J
(2)由功能关系可知,电动机做的功等于物块增加的机械能和因滑动摩擦而发的热,所以:
相对滑动时:S相=v?
| v |
| a |
所以,由功能关系得:W电=(mgLsinθ+
| 1 |
| 2 |
答:(1)传送带对物体所做的功为255J;(2)电动机所做的功为270J.
点评:本题为传送带问题,要注意分析物体在传送带上的受力情况及运动情况,综合利用牛顿第二定律及动能定理、功能关系等方法求解.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 如图所示为一皮带传送装置,皮带保持匀速率运动,货物由静止放到传送带上,被传送带向下传送,其运动的v-t图象如图乙所示.
如图所示为一皮带传送装置,皮带保持匀速率运动,货物由静止放到传送带上,被传送带向下传送,其运动的v-t图象如图乙所示.