题目内容
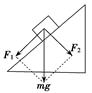
如图所示,细线的一端系一质量为m的小球,另一端固定在倾角为θ的光滑斜面体顶端,细线与斜面平行。在斜面体以加速度a水平向右做匀加速直线运动的过程中,小球始终静止在斜面上,小球受到细线的拉力T和斜面的支持力为FN分别为(重力加速度为g)


| A.T=m(gsinθ+ acosθ),FN=m(gcosθ- asinθ) |
| B.T=m(gsinθ+ acosθ),FN=m(gsinθ- acosθ) |
| C.T=m(acosθ- gsinθ),FN=m(gcosθ+ asinθ) |
| D.T=m(asinθ- gcosθ),FN=m(gsinθ+ acosθ) |
A
对球受力分析如图所示,沿水平方向和竖直方向正交分解:

水平方向:Tcosθ-FNsinθ=ma;竖直方向:Tsinθ+FNcosθ=mg。
联立两式,解得:T=m(gsinθ+ acosθ),FN=m(gcosθ- asinθ),故A正确。
【方法技巧】本题可以令a=0(特殊值代入法),利用小球的平衡条件可得T=mgsinθ,FN= mgcosθ,经检验只有选项A正确。
【考点定位】受力分析、力的分解、牛顿第二定律。

水平方向:Tcosθ-FNsinθ=ma;竖直方向:Tsinθ+FNcosθ=mg。
联立两式,解得:T=m(gsinθ+ acosθ),FN=m(gcosθ- asinθ),故A正确。
【方法技巧】本题可以令a=0(特殊值代入法),利用小球的平衡条件可得T=mgsinθ,FN= mgcosθ,经检验只有选项A正确。
【考点定位】受力分析、力的分解、牛顿第二定律。

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
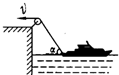

 、
、 质量分别是
质量分别是 和
和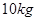 ,不计滑轮与绳间摩擦及绳的重力,若整个系统静止,
,不计滑轮与绳间摩擦及绳的重力,若整个系统静止, 取
取 。求:
。求: