题目内容
19. 正三角形ABC的三个顶点处分别有垂直于三角形平面的无限长直导线,导线中通有恒定电流,方向如图所示,a、b、c三点分别是正三角形三边的中点,若A、B、C三处导线中的电流分别为l、2l、3l,已知无限长直导线在其周围某一点产生的磁场磁感应强度B的大小与电流成正比,与电流到这一点的距离成反比,即B=$k\frac{I}{r}$,则a、b、c三点的磁感应强度大小关系为( )
正三角形ABC的三个顶点处分别有垂直于三角形平面的无限长直导线,导线中通有恒定电流,方向如图所示,a、b、c三点分别是正三角形三边的中点,若A、B、C三处导线中的电流分别为l、2l、3l,已知无限长直导线在其周围某一点产生的磁场磁感应强度B的大小与电流成正比,与电流到这一点的距离成反比,即B=$k\frac{I}{r}$,则a、b、c三点的磁感应强度大小关系为( )| A. | a点最大 | B. | b点最大 | C. | c点最大 | D. | b,c两点一样大 |
分析 本题考查了磁场的叠加,根据导线周围磁场分布可知,与导线等距离地方磁感应强度大小相等,根据安培定则判断出两导线在a、b、c三点形成磁场方向,磁感应强度B是矢量,根据矢量分解合成的平行四边形定则求解.
解答 解:设正三角形的边长为2L,
根据公式B=$k\frac{I}{r}$,结合矢量的叠加原理,
则a、b、c三点的磁感应强度大小分别为
Ba=4k$\frac{I}{L}$;
Bb=$\sqrt{(\frac{kI}{\sqrt{3}L})^{2}+(\frac{5kI}{L})^{2}}$=$\sqrt{\frac{76}{3}}k\frac{I}{L}$
Bc=$\sqrt{(\frac{2kI}{\sqrt{3}L})^{2}+(\frac{4kI}{L})^{2}}$=$\sqrt{\frac{52}{3}}k\frac{I}{L}$
综上所述,故B正确,ACD错误;
故选:B.
点评 磁感应强度为矢量,合成时要用平行四边形定则,因此要正确根据安培定则判断导线周围磁场方向是解题的前提.

练习册系列答案
相关题目
9.某物体做直线运动的v-t图象如图所示.则关于物体在前8s内的运动,下列说法正确的是( )


| A. | 物体一直沿同一方向运动 | |
| B. | 4s-6s内的加速度等于6s-8s内的加速度 | |
| C. | 前8s内的位移为4m | |
| D. | 第8s末物体离出发点最远 |
4. 光滑金属导轨宽L=0.5m,电阻不计,均匀变化的磁场充满整个轨道平面,如图甲所示,磁场的磁感应强度随时间变化的情况如图乙所示.金属棒ab的电阻为2Ω,垂直固定在导轨上静止不动,且与导轨左端距离l=0.2m,则( )
光滑金属导轨宽L=0.5m,电阻不计,均匀变化的磁场充满整个轨道平面,如图甲所示,磁场的磁感应强度随时间变化的情况如图乙所示.金属棒ab的电阻为2Ω,垂直固定在导轨上静止不动,且与导轨左端距离l=0.2m,则( )
 光滑金属导轨宽L=0.5m,电阻不计,均匀变化的磁场充满整个轨道平面,如图甲所示,磁场的磁感应强度随时间变化的情况如图乙所示.金属棒ab的电阻为2Ω,垂直固定在导轨上静止不动,且与导轨左端距离l=0.2m,则( )
光滑金属导轨宽L=0.5m,电阻不计,均匀变化的磁场充满整个轨道平面,如图甲所示,磁场的磁感应强度随时间变化的情况如图乙所示.金属棒ab的电阻为2Ω,垂直固定在导轨上静止不动,且与导轨左端距离l=0.2m,则( )| A. | 1s末回路中的电动势为0.1V | B. | 1s末回路中的电流为1A | ||
| C. | 2s末回路产生的电热为0.01J | D. | 2s末,ab所受安培力大小为0.05N |
11.下列关于力的说法中正确的是( )
| A. | 力一定发生在相互接触的两个物体之间 | |
| B. | 重力方向总是垂直于接触面向下 | |
| C. | 弹力产生在直接接触且发生弹性形变的物体之间 | |
| D. | 摩擦力总是阻碍物体运动的 |
8.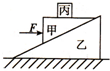 如图所示,甲、丙物体在水平外力F的作用下静止在乙物体上,乙物体静止在水平面上.现增大水平外力F,三物体仍然静止,则下列说法正确的是( )
如图所示,甲、丙物体在水平外力F的作用下静止在乙物体上,乙物体静止在水平面上.现增大水平外力F,三物体仍然静止,则下列说法正确的是( )
 如图所示,甲、丙物体在水平外力F的作用下静止在乙物体上,乙物体静止在水平面上.现增大水平外力F,三物体仍然静止,则下列说法正确的是( )
如图所示,甲、丙物体在水平外力F的作用下静止在乙物体上,乙物体静止在水平面上.现增大水平外力F,三物体仍然静止,则下列说法正确的是( )| A. | 乙对甲的支持力一定增大 | B. | 乙对地面的压力一定不变 | ||
| C. | 乙对甲的摩擦力一定增大 | D. | 甲对丙的摩擦力一直为零 |
9.如图甲所示,一条电场线与Ox轴重合,取O点电势为零,Ox方向上各点的电势φ随x变化的情况如图乙所示.若在O点由静止释放一电子,电子仅受电场力的作用,则( )


| A. | 电子一直沿Ox负方向运动 | B. | 电子运动的加速度逐渐增大 | ||
| C. | 电场力一直做正功 | D. | 电子的电势能逐渐增大 |
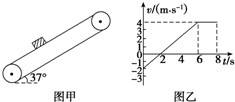 如图甲所示,一倾角为37°的传送带以恒定速度运行,现将一质量m=1kg的小物体抛上传送带,物体相对地面的速度随时间变化的关系如图乙所示,取沿传送带向上为正方向,g=10m/s2,sin 37°=0.6,cos 37°=0.8.求:
如图甲所示,一倾角为37°的传送带以恒定速度运行,现将一质量m=1kg的小物体抛上传送带,物体相对地面的速度随时间变化的关系如图乙所示,取沿传送带向上为正方向,g=10m/s2,sin 37°=0.6,cos 37°=0.8.求: 板之间的滑动摩擦力,将黑板上的粉笔字擦干净,已知黑板的规格是:4.5m×1.5m2,黑板的下边沿离地的高度为0.8m,若小黑板擦(可视为质点)的质量为0.1kg,现假定某同学用力将黑板擦在黑板表面匀速竖直向上擦黑板,当手臂对小黑板擦的作用力F与黑板面成θ=53°时,F=5N,他所能擦到的离地最大高度为2.05m,(g取10m/s2,sin53°=0.8,cos53°=0.6)求:
板之间的滑动摩擦力,将黑板上的粉笔字擦干净,已知黑板的规格是:4.5m×1.5m2,黑板的下边沿离地的高度为0.8m,若小黑板擦(可视为质点)的质量为0.1kg,现假定某同学用力将黑板擦在黑板表面匀速竖直向上擦黑板,当手臂对小黑板擦的作用力F与黑板面成θ=53°时,F=5N,他所能擦到的离地最大高度为2.05m,(g取10m/s2,sin53°=0.8,cos53°=0.6)求: