题目内容
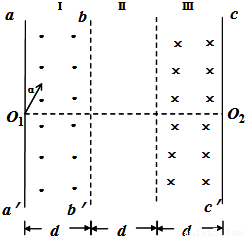
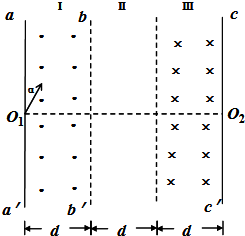如图所示，有三个宽度均为d的区域I、Ⅱ、Ⅲ；在区域I和Ⅲ内分别为方向垂直于纸面向外和向里的匀强磁场（虚线为磁场边界面，并不表示障碍物），区域I磁感应强度大小为B，某种带正电的粒子，从孔O1以大小不同的速度沿图示与aa'夹角α=30°的方向进入磁场（不计重力），已知速度为υo和2υo时，粒子在区域I内的运动时间相同，均为to；速度为υ时粒子在区域I内的运时间为| to |
| 5 |
（1）粒子的比荷
| q |
| m |
（2）若区域Ⅲ磁感应强度大小也为B，速度为υ的粒子打到边界cc'上的位置P点到O2点的距离；
（3）若在图中区域Ⅱ中O1O2上方加竖直向下的匀强电场，O1O2下方对称加竖直向上的匀强电场，场强大小相等，使速度为υ的粒子每次均垂直穿过I、Ⅱ、Ⅲ区域的边界面并能回到O1点，则所加电场场强和区域Ⅲ磁感应强度大小为多大？并求出粒子在场中运动的总时间．
分析：（1）速度为υo和2υo时粒子在区域I内的运动时间相同，故粒子运动的轨迹对应的圆心角相同，故只能在区域I中运动，故其轨迹所对应的圆心角为300°=
，根据周期公式通过运动的时间求出粒子的比荷．速度为υ时粒子在区域I内的运时间为
，求出对应的圆心角，根据粒子的半径结合几何关系求出区域I的宽度d．
（2）根据运动的对称性，结合几何关系求出速度为υ的粒子打到边界cc'上的位置P点到O2点的距离．
（3）度为υ的粒子每次均垂直穿过I、Ⅱ、Ⅲ区域的边界面并能回到O1点，根据要求作出运动的轨迹图，根据粒子在电场中做类平抛运动，结合运动的周期性求出电场强度的大小，进入磁场做匀速圆周运动，在磁场中运动180°出磁场，根据半径的大小关系求出磁感应强度的大小．分别求出粒子在电场中和磁场中运动的时间，从而求出总时间．
| 5π |
| 3 |
| to |
| 5 |
（2）根据运动的对称性，结合几何关系求出速度为υ的粒子打到边界cc'上的位置P点到O2点的距离．
（3）度为υ的粒子每次均垂直穿过I、Ⅱ、Ⅲ区域的边界面并能回到O1点，根据要求作出运动的轨迹图，根据粒子在电场中做类平抛运动，结合运动的周期性求出电场强度的大小，进入磁场做匀速圆周运动，在磁场中运动180°出磁场，根据半径的大小关系求出磁感应强度的大小．分别求出粒子在电场中和磁场中运动的时间，从而求出总时间．
解答：解：（1）带电粒子在磁场中做匀速圆周运动，故有：qvB=
，解得：R=
，
根据运动的周期：T=
可得粒子运动的周期：T=
由速度为υo和2υo时粒子在区域I内的运动时间相同，故粒子运动的轨迹对应的圆心角相同，故只能在区域I中运动，故其轨迹所对应的圆心角为300°=
，所以根据
=
，解得：t0=
T=
所以粒子的比荷：
=
当速度为v时，t=
，则轨迹对应的圆心角θ=60°，而此时粒子的轨道半径：R=
，
所以区域I的宽度为：d=Rsin60°=
（2）lo2p=2(R-Rcos60°)=
（3）粒子做类平抛运动，有：
=
t2
根据运动的对称性及周期性知：2x+4nx=d（n=0、1、2、3…）
x=vt
得E=
Bv(2n+1)2 B'=2B
t电=
=
t磁=
+
=
t0
综上 t=
t0+
．
答：（1）粒子的比荷
为
．区域I的宽度d为
．
（2）速度为υ的粒子打到边界cc'上的位置P点到O2点的距离
．
（3）所加的电场强度E=
Bv(2n+1)2，磁感应强度大小为2B．粒子在场中运动的总时间t=
t0+
．
| mv2 |
| R |
| mv |
| qB |
根据运动的周期：T=
| 2πR |
| v |
| 2πm |
| qB |
由速度为υo和2υo时粒子在区域I内的运动时间相同，故粒子运动的轨迹对应的圆心角相同，故只能在区域I中运动，故其轨迹所对应的圆心角为300°=
| 5π |
| 3 |
| t0 |
| T |
| ||
| 2π |
| 5 |
| 6 |
| 5πm |
| 3qB |
所以粒子的比荷：
| q |
| m |
| 5π |
| 3Bt0 |
当速度为v时，t=
| t0 |
| 5 |
| mv |
| qB |
所以区域I的宽度为：d=Rsin60°=
3
| ||
| 10π |
（2）lo2p=2(R-Rcos60°)=
| 3vt0 |
| 5π |
（3）粒子做类平抛运动，有：
| R |
| 2 |
| Eq |
| 2m |
根据运动的对称性及周期性知：2x+4nx=d（n=0、1、2、3…）
x=vt
得E=
| 16 |
| 3 |
t电=
| 2d |
| v |
3
| ||
| 5π |
t磁=
| T |
| 3 |
| T |
| 2 |
| 7 |
| 10 |
综上 t=
| 7 |
| 10 |
3
| ||
| 5π |
答：（1）粒子的比荷
| q |
| m |
| 5π |
| 3Bt0 |
3
| ||
| 10π |
（2）速度为υ的粒子打到边界cc'上的位置P点到O2点的距离
| 3vt0 |
| 5π |
（3）所加的电场强度E=
| 16 |
| 3 |
| 7 |
| 10 |
3
| ||
| 5π |
点评：带电粒子在匀强磁场中的运动是整个高中的重点，也是高考的必考的内容，粒子的运动过程的分析是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
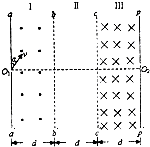（2013?福建模拟）如图所示，有三个宽度均为d的区域Ⅰ、Ⅱ、Ⅲ；在区域Ⅰ和Ⅲ内分别有方向垂直于纸面向外和向里的匀强磁场（虚线为磁场边界，并不表示障碍物），区域Ⅰ中磁场的磁感应强度大小为B，区域Ⅲ中磁场的磁感应强度大小未知．质量为m、带电量为+q的粒子，从孔O1以大小不同的速率沿图示与aa′夹角a=30°的方向进入磁场，粒子重力忽略不计．
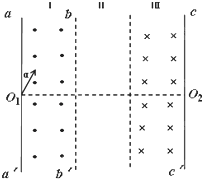如图所示，有三个宽度均相等的区域I、Ⅱ、Ⅲ；在区域I和Ⅲ内分别为方向垂直于纸面向外和向里的匀强磁场（虚线为磁场边界面，并不表示障碍物），区域I磁感应强度大小为B，某种带正电的粒子，从孔O1以大小不同的速度沿图示与aa′夹角α=300的方向进入磁场（不计重力）．已知速度为v0和2v0时，粒子仅在区域I内运动且运动时间相同，均为t0．
。求：
和区域I的宽度d；
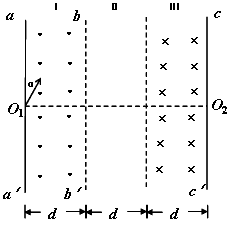
．求：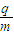
和区域I的宽度d；