题目内容
20.下列各组数据中,能计算出地球质量的是( )| A. | 地球绕太阳运行的周期及日、地间距离 | |
| B. | 月球绕地球运行的周期及月、地间距离 | |
| C. | 人造地球卫星在近地轨道的绕行速度 | |
| D. | 地球同步卫星离地面的高度 |
分析 地球质量的估算有两种方法:(1)在地球上的物体可由万有引力等于向心力进行计算;(2)围绕地球做匀速圆周运动可由万有引力提供向心力进行计算.
解答 解:A、地球绕太阳做圆周运动,万有引力提供向心力,由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=m$(\frac{2π}{T})^{2}$r,其中:M为太阳的质量,m为地球的质量,解得:M=$\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$,能估算太阳的质量,不能求出地球的质量,故A错误.
B、月球绕地球做圆周运动,万有引力提供向心力,由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=m$(\frac{2π}{T})^{2}$r,其中:M为地球的质量,m为月球的质量,解得:M=$\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$,已知:月球绕地球运行的周期T及月、地间距离r,可以求出地球的质量,故B正确.
C、人造地球卫星绕地球做圆周运动,万有引力提供向心力,由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=m$(\frac{2π}{T})^{2}$r,其中:M为地球的质量,m为人造地球卫星的质量,解得:M=$\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$,已知:人造地球卫星绕地球运行的周期T及月、地间距离r,可以求出地球的质量,故C正确.
D、由:M=$\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$可知,只知道地球同步卫星离地面的高度h,不知道地球半径R,估算不出地球的质量.故D错误;
故选:BC.
点评 星球质量的估算有两种方法:(1)在星球上的物体可由万有引力等于向心力进行计算;(2)围绕星球做匀速圆周运动可由万有引力提供向心力进行计算.找到合适的公式既可.

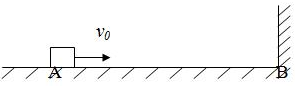
| A. | 40m | B. | 37.5m | C. | 30m | D. | 35m |
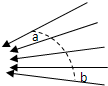 如图所示,实线为某区域电场的电场线,虚线是某一带电粒子只在电场力作用下通过该电场区域时的运动轨迹,a、b是轨迹上的两点.下列判断正确的是( )
如图所示,实线为某区域电场的电场线,虚线是某一带电粒子只在电场力作用下通过该电场区域时的运动轨迹,a、b是轨迹上的两点.下列判断正确的是( )| A. | 带电粒子为正电荷 | B. | a、b两点的电势:ϕa>ϕb | ||
| C. | 带电粒子在a点的加速度比b点小 | D. | 带电粒子在a点的电势能比b点小 |
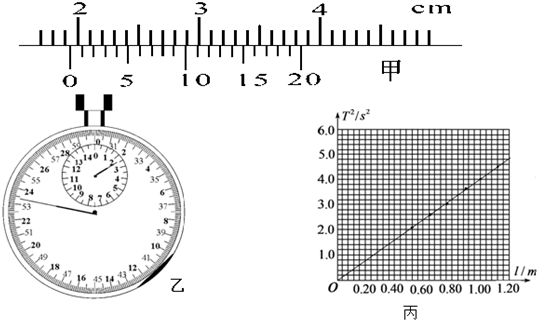
 如图所示,质量为m=50g,长L=10cm的铜棒,用长度相等的两根轻软导线悬吊在竖直向上的匀强磁场中,导线跟铜棒的接触良好,磁感应强度B=0.5T.当导线中通入某恒定电流后,铜棒恰好偏离竖直方向37°而静止.求:铜棒中所通恒定电流的大小和方向.(g=10m/s2,sin37°=0.6,cos37°=0.8)
如图所示,质量为m=50g,长L=10cm的铜棒,用长度相等的两根轻软导线悬吊在竖直向上的匀强磁场中,导线跟铜棒的接触良好,磁感应强度B=0.5T.当导线中通入某恒定电流后,铜棒恰好偏离竖直方向37°而静止.求:铜棒中所通恒定电流的大小和方向.(g=10m/s2,sin37°=0.6,cos37°=0.8)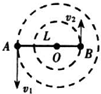 如图所示,一双星A、B,绕它们连线上的一点做匀速圆周运动,其运行周期为T,A、B间的距离为L,它们的线速度之比$\frac{{v}_{1}}{{v}_{2}}$=2,试求其中m1的质量m1=$\frac{4{π}^{2}{L}^{3}}{3G{T}^{2}}$.
如图所示,一双星A、B,绕它们连线上的一点做匀速圆周运动,其运行周期为T,A、B间的距离为L,它们的线速度之比$\frac{{v}_{1}}{{v}_{2}}$=2,试求其中m1的质量m1=$\frac{4{π}^{2}{L}^{3}}{3G{T}^{2}}$.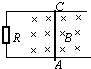 如图所示,一U形金属框的可动边AC长0.1m,匀强磁场的磁感强度为0.5T,AC以8m/s的速度水平向右移动,电阻R为5Ω,(其它电阻均不计).
如图所示,一U形金属框的可动边AC长0.1m,匀强磁场的磁感强度为0.5T,AC以8m/s的速度水平向右移动,电阻R为5Ω,(其它电阻均不计). 小车上固定一根弹性直杆A,杆顶固定一个小球B(如图所示),先让小车从光滑斜面上自由下滑,在下图的情况中杆发生了不同的形变,其中正确的是( )
小车上固定一根弹性直杆A,杆顶固定一个小球B(如图所示),先让小车从光滑斜面上自由下滑,在下图的情况中杆发生了不同的形变,其中正确的是( )