题目内容
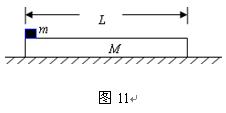
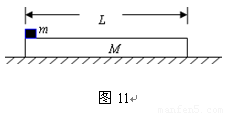
如图11所示,质量m=2.0×10-4kg、电荷量q=1.0×10-6C的带正电微粒静止在空间范围足够大的匀强电场中,电场强度大小为E1。在t=0时刻,电场强度突然增加到E2=4.0×103N/C,到t=0.20s时再把电场方向改为水平向右,场强大小保持不变。取g=10m/s2。取g=10m/s2。求:
(1)t=0.20s时间内带电微粒上升的高度;
(2)t=0.20s时间内带电微粒增加的电势能;
(3)电场方向改为水平向右后带电微粒的最小动能。

(1)在E2电场中,设带电微粒向上的加速度为a1,根据牛顿第二定律
q E2-mg=ma1
解得:a1=10m/s2
设0.20s时间内带电微粒上升的高度为h,则
![]()
解得:h=0.20m
(2)在t=0.20s时间内电场力对带电微粒做正功,电势能减少
![]()
解得:ΔE=-8.0×10-2J
(3)在t=0.20s时带点微粒的速度v1=a1t=2.0m/s
把电场E2改为水平向右后,设带电微粒在竖直方向做匀减速运动的速度为vy,水平方向作匀加速运动的速度为vx,带电微粒的动能达到最小时所用时间为t1,则
vy=v1-gt1
vx=a2t1,
a2=![]() =20m/s
=20m/s
解得:vy=2.0-10t1, vx=20t1
带点微粒的动能Ek=![]()
![]()
![]()
当![]() =0.04 s时,Ek有最小值
=0.04 s时,Ek有最小值
解得:Ek=3.2×10-4J
说明:用当电场力与重力的合力与速度方向垂直时,速度有最小值,计算也可以。

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目