题目内容
消防队员在某高楼进行训练,他要从距地面高h=36m处的一扇窗户外沿一条竖直悬挂的绳子滑下,在下滑过程中,他先匀加速下滑,此时手脚对悬绳的压力 =640N,紧接着再匀减速下滑,此时手脚对悬绳的压力
=640N,紧接着再匀减速下滑,此时手脚对悬绳的压力 =2080N,滑至地面时速度恰为0。已知消防队员的质量为m=80kg,手脚和悬绳间的动摩擦因数为μ=0.5,g=10m/s2,求:
=2080N,滑至地面时速度恰为0。已知消防队员的质量为m=80kg,手脚和悬绳间的动摩擦因数为μ=0.5,g=10m/s2,求:
(1)分别求出他在加速下滑、减速下滑两过程中的加速度大小?
(2)他沿绳滑至地面所用的总时间t?
 =640N,紧接着再匀减速下滑,此时手脚对悬绳的压力
=640N,紧接着再匀减速下滑,此时手脚对悬绳的压力 =2080N,滑至地面时速度恰为0。已知消防队员的质量为m=80kg,手脚和悬绳间的动摩擦因数为μ=0.5,g=10m/s2,求:
=2080N,滑至地面时速度恰为0。已知消防队员的质量为m=80kg,手脚和悬绳间的动摩擦因数为μ=0.5,g=10m/s2,求:(1)分别求出他在加速下滑、减速下滑两过程中的加速度大小?
(2)他沿绳滑至地面所用的总时间t?
(1)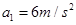
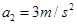 (2)
(2) 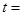 6s
6s
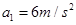
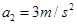 (2)
(2) 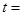 6s
6s本题考查牛顿第二定律和多过程问题,分析消防队员受力情况,由牛顿第二定律求出两个过程的加速度,再由运动学相关公式求解
(1)设消防队员匀加速下滑的加速度大小为a1, 匀减速下滑的加速度大小为a2,根据牛顿第二定律,得
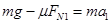 2分
2分
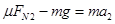 2分
2分
解得,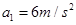 1分
1分
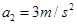 1分
1分
(2)设加速过程时间为t1,减速过程时间为t2,根据匀变速运动规律,有
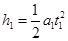 2分
2分
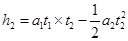 2分
2分
又 1分
1分
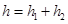 1分
1分
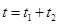 1分
1分
联立以上各式并代入数据解得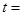 6s 1分
6s 1分
(1)设消防队员匀加速下滑的加速度大小为a1, 匀减速下滑的加速度大小为a2,根据牛顿第二定律,得
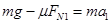 2分
2分 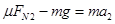 2分
2分解得,
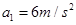 1分
1分 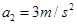 1分
1分(2)设加速过程时间为t1,减速过程时间为t2,根据匀变速运动规律,有
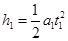 2分
2分 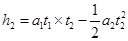 2分
2分又
 1分
1分 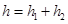 1分
1分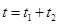 1分
1分联立以上各式并代入数据解得
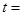 6s 1分
6s 1分
练习册系列答案
相关题目
 mg
mg






