题目内容
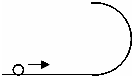
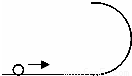
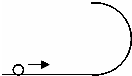 (选做C)如图所示,一水平轨道与一竖直半圆轨道相接,半圆轨道半径为R=1.6m,小球沿水平轨道进入半圆轨道,恰能从半圆轨道顶端水平射出.求:
(选做C)如图所示,一水平轨道与一竖直半圆轨道相接,半圆轨道半径为R=1.6m,小球沿水平轨道进入半圆轨道,恰能从半圆轨道顶端水平射出.求:(1)小球射出后在水平轨道上的落点与出射点的水平距离.
(2)小球落到水平轨道上时的速度大小.(g取得10m/s2)
分析:小球恰能从半圆轨道顶端水平射出,则在最高点由重力提供向心力,小球抛出后做平抛运动,根据高度求出平抛运动的时间,再根据初速度和时间求出平抛运动的水平位移.求出落地时竖直方向的速度,根据速度合成原则求出落地时的速度.
解答:解:(1)小球恰能从半圆轨道顶端水平射出,则在最高点由重力提供向心力
mg=m
解得:v=
=4m/s
小球抛出后做平抛运动,
t=
=
=0.8s
所以水平距离为:x=vt=3.2m
(2)小球落地时竖直方向速度为;vy=gt=8m/s
所以落地时的速度为
=4
m/s
答:(1)小球射出后在水平轨道上的落点与出射点的水平距离为3.2m.
(2)小球落到水平轨道上时的速度大小为4
m/s
mg=m
| v2 |
| r |
解得:v=
| gr |
小球抛出后做平抛运动,
t=
|
|
所以水平距离为:x=vt=3.2m
(2)小球落地时竖直方向速度为;vy=gt=8m/s
所以落地时的速度为
| v2+vy2 |
| 5 |
答:(1)小球射出后在水平轨道上的落点与出射点的水平距离为3.2m.
(2)小球落到水平轨道上时的速度大小为4
| 5 |
点评:本题主要考查了向心力公式及平抛运动基本公式的直接应用,难度适中.

练习册系列答案
相关题目