题目内容
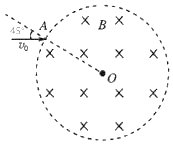
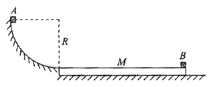
【题目】如图所示,往光滑的水平而上有M=2kg的长木板,在其右端放一个质量m=1kg、可视为质点的物体B,长木板的左上端恰与一个固定在紧直面内半径R=1.25m的光滑![]() 圆弧底端平齐,现将一个质量m=1Kg、可视为质点的物体A从圆弧最高点由静止滑下。己知物体A与长木板间的动摩擦因数为0.4,物体B与长木板间的动摩擦因数为0.2。当物体A刚滑上长木板时对物体B施加一大小为I=1N·s、方向向左的瞬时冲量,结果两物体在长木板上恰好不相撞。取g=10m/s2,求:
圆弧底端平齐,现将一个质量m=1Kg、可视为质点的物体A从圆弧最高点由静止滑下。己知物体A与长木板间的动摩擦因数为0.4,物体B与长木板间的动摩擦因数为0.2。当物体A刚滑上长木板时对物体B施加一大小为I=1N·s、方向向左的瞬时冲量,结果两物体在长木板上恰好不相撞。取g=10m/s2,求:
(1)全程因摩擦而产生的热量:
(2)长木板的长度。
【答案】(1)11J(2)3m
【解析】
(1)物体A沿圆弧下滑,由动能定理得:mgR=![]()
可得:vA=5m/s
对B,由动量定理得:I=mvB。
解得:vB=1m/s
两物体恰不相撞时整体同速,取水平向右为正方向,由动量守恒定律得:
mvA-I=(M+m+m)v
解得:v=1m/s
由功能关系得:![]()
解得:Q=11J
(2)物体B在长木板上减至0的时间为:![]()
![]()
由对称性知物体B反向加速至v=1m/s的过程中,t2=t1=![]() s,
s, ![]()
对地位移为0。
长木板在t1、t2时间内的加速度为 ![]()
解得 a=1m/s2
对应的位移为x3=![]() a(t1+t2)2
a(t1+t2)2
解得 x3=![]() m
m
相对滑动时间内物体A一直匀减速的位移为 ![]()
解得 x4=3m
由几何关系知长木板的长度 L=x4-x3+x3=3m

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目