题目内容
(2009?浙江)某校物理兴趣小组决定举行遥控赛车比赛.比赛路径如图所示,赛车从起点A出发,沿水平直线轨道运动L后,由B点进入半径为R的光滑竖直圆轨道,离开竖直圆轨道后继续在光滑平直轨道上运动到C点,并能越过壕沟.已知赛车质量m=0.1kg,通电后以额定功率P=1.5w工作,进入竖直轨道前受到阻力恒为0.3N,随后在运动中受到的阻力均可不记.图中L=10.00m,R=0.32m,h=1.25m,S=2.50m.问:要使赛车完成比赛,电动机至少工作多长时间?(取g=10m/s2 )


分析:本题赛车的运动可以分为三个过程,由A至B的过程可以运用动能定理列式,在圆轨道上的过程机械能守恒,也可以用动能定理列式,以及平抛运动的过程;本题有两个约束条件,即要能越过壕沟,同时要能到达轨道的最高点.
解答:解:设赛车越过壕沟需要的最小速度为v1,由平抛运动的规律
s=v1t
h=
gt2
解得
v1=s
=5m/s
设赛车恰好越过圆轨道,对应圆轨道最高点的速度为v2,最低点的速度为v3,由牛顿第二定律及机械能守恒定律
mg=m
m
=
m
+mg(2R)
解得 v3=
=4m/s (
由于B点以后的轨道均为光滑,故轨道最低点速度应该等于平抛的初速度,通过分析比较,赛车要完成比赛,在进入圆轨道前的速度最小应该是
vmin=5m/s
设电动机工作时间至少为t,根据功能原理
pt-fL=
m
由此可得 t=
s
即要使赛车完成比赛,电动机至少工作
s的时间.
s=v1t
h=
| 1 |
| 2 |
解得
v1=s
|
设赛车恰好越过圆轨道,对应圆轨道最高点的速度为v2,最低点的速度为v3,由牛顿第二定律及机械能守恒定律
mg=m
| ||
| R |
| 1 |
| 2 |
| v | 2 3 |
| 1 |
| 2 |
| v | 2 2 |
解得 v3=
| 5gh |
由于B点以后的轨道均为光滑,故轨道最低点速度应该等于平抛的初速度,通过分析比较,赛车要完成比赛,在进入圆轨道前的速度最小应该是
vmin=5m/s
设电动机工作时间至少为t,根据功能原理
pt-fL=
| 1 |
| 2 |
| v | 2 min |
由此可得 t=
| 17 |
| 6 |
即要使赛车完成比赛,电动机至少工作
| 17 |
| 6 |
点评:本题是力电综合问题,关键要将物体的运动分为三个过程,分析清楚各个过程的运动特点和受力特点,然后根据动能定理、平抛运动公式、向心力公式列式求解!

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目

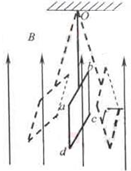 (2009?浙江)如图所示,在磁感应强度大小为B、方向竖直向上的匀强磁场中,有一质量为m、阻值为R的闭合矩形金属线框abcd用绝缘轻质细杆悬挂在O点,并可绕O点摆动.金属线框从右侧某一位置静止开始释放,在摆动到左侧最高点的过程中,细杆和金属框平面始终处于同一平面,且垂直纸面.则线框中应电流的方向是( )
(2009?浙江)如图所示,在磁感应强度大小为B、方向竖直向上的匀强磁场中,有一质量为m、阻值为R的闭合矩形金属线框abcd用绝缘轻质细杆悬挂在O点,并可绕O点摆动.金属线框从右侧某一位置静止开始释放,在摆动到左侧最高点的过程中,细杆和金属框平面始终处于同一平面,且垂直纸面.则线框中应电流的方向是( )