题目内容
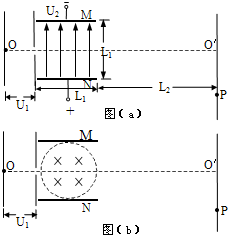
如图(a)所示,电子从加速电场的O点发出(初速不计),经电压为U1的加速电场加速后沿中心线进入两平行金属板M、N间的匀强电场中,通过电场后打到荧光屏上的P点处,设M、N板间的电压为U2,两极板间距离与板长相等,均为L1,板的右端到荧光屏的距离为L2,已知U1=200V,U2=300V,L1=6cm,L2=21cm,电子的比荷e/m=1.8×1011C/kg.求:(1)电子离开偏转电场时的偏角θ的正切函数值tanθ(若可以求出具体角度也行);
(2)电子打到荧光屏上的位置P偏离荧光屏中心O′的距离Y;
(3)若撤去M、N间的电压U2,而在两平行板间直径为L1的圆形区域内加一方向垂直纸面向里的匀强磁场(如图b所示,圆心恰好在平行板的正中间),要使电子通过磁场后仍打在荧光屏上的P点处,则电子在磁场中的轨道半径为多大?磁感应强度B的大小为多大?
【答案】分析:(1)直线加速阶段,运用动能定理列式求解;类似平抛运动阶段,根据速度偏转角度正切值公式列式求解;
(2)根据列式平抛运动的分位移公式求解偏移量y,然后运用“速度的反向延长线通过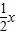 ”的结论并结合几何关系列式求解;
”的结论并结合几何关系列式求解;
(3)画出运动轨迹后,结合几何关系求解出半径;然后根据洛伦兹力提供向心力列式求解磁感应强度.
解答:解:(1)对加速阶段应用动能定理,有:
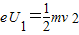
解得:v=
偏转阶段类平抛轨迹如图a所示,可以得到:

所以θ=37°
(2)经过偏转电场时的偏转距离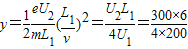 cm=2.25cm
cm=2.25cm
从偏转电场出来后作直线运动:由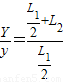
得Y=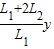 =
=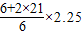 cm=18cm
cm=18cm
[或直接求Y=(L2+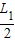 )tanθ=(21+3)×
)tanθ=(21+3)× cm=18cm]
cm=18cm]
(3)如图乙所示,电子轨迹从磁场出来的切线延长线交于磁场区的圆心,因为也打在P点,所以θ=37°
由图可知电子轨道半径R满足:
Rsinθ=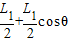
解之得:
R=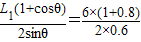 cm=9cm
cm=9cm
又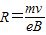
得B=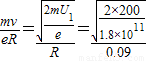 =
=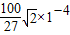 =5.24×10-4T
=5.24×10-4T
答:(1)电子离开偏转电场时的偏角θ的正切函数值tanθ为 ;
;
(2)电子打到荧光屏上的位置P偏离荧光屏中心O′的距离Y为18cm;
(3)电子在磁场中的轨道半径为9cm,磁感应强度B的大小为5.24×10-4T.
点评:本题要明确粒子的运动规律,然后分阶段运用动能定理、类平抛运动规律、牛顿第二定律列式求解,关键是画出运动轨迹,较难.
(2)根据列式平抛运动的分位移公式求解偏移量y,然后运用“速度的反向延长线通过
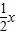 ”的结论并结合几何关系列式求解;
”的结论并结合几何关系列式求解;(3)画出运动轨迹后,结合几何关系求解出半径;然后根据洛伦兹力提供向心力列式求解磁感应强度.
解答:解:(1)对加速阶段应用动能定理,有:
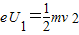
解得:v=

偏转阶段类平抛轨迹如图a所示,可以得到:

所以θ=37°
(2)经过偏转电场时的偏转距离
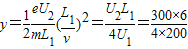 cm=2.25cm
cm=2.25cm 从偏转电场出来后作直线运动:由
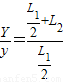
得Y=
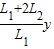 =
=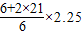 cm=18cm
cm=18cm [或直接求Y=(L2+
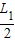 )tanθ=(21+3)×
)tanθ=(21+3)× cm=18cm]
cm=18cm](3)如图乙所示,电子轨迹从磁场出来的切线延长线交于磁场区的圆心,因为也打在P点,所以θ=37°
由图可知电子轨道半径R满足:
Rsinθ=
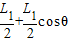
解之得:
R=
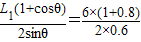 cm=9cm
cm=9cm 又
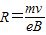
得B=
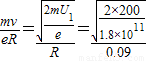 =
=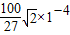 =5.24×10-4T
=5.24×10-4T 答:(1)电子离开偏转电场时的偏角θ的正切函数值tanθ为
 ;
;(2)电子打到荧光屏上的位置P偏离荧光屏中心O′的距离Y为18cm;
(3)电子在磁场中的轨道半径为9cm,磁感应强度B的大小为5.24×10-4T.
点评:本题要明确粒子的运动规律,然后分阶段运用动能定理、类平抛运动规律、牛顿第二定律列式求解,关键是画出运动轨迹,较难.

练习册系列答案
相关题目
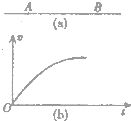 如图(a)所示:AB是某电场中的一条电场线,若在A点放置一初速度为零的电子,电子仅在电场力的作用下,沿AB由A运动到B过程中的速度图象如图(b)所示,则下列关于A、B两点电势φ和电场强度E的判断中正确的是( )
如图(a)所示:AB是某电场中的一条电场线,若在A点放置一初速度为零的电子,电子仅在电场力的作用下,沿AB由A运动到B过程中的速度图象如图(b)所示,则下列关于A、B两点电势φ和电场强度E的判断中正确的是( )| A、φA>φB,EA>EB | B、φA>φB,EA<EB | C、φA<φB,EA>EB | D、φA<φB,EA<EB |
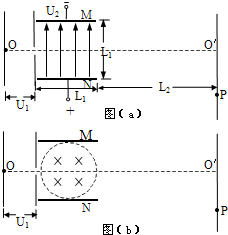 如图(a)所示,电子从加速电场的O点发出(初速不计),经电压为U1的加速电场加速后沿中心线进入两平行金属板M、N间的匀强电场中,通过电场后打到荧光屏上的P点处,设M、N板间的电压为U2,两极板间距离与板长相等,均为L1,板的右端到荧光屏的距离为L2,已知U1=200V,U2=300V,L1=6cm,L2=21cm,电子的比荷e/m=1.8×1011C/kg.求:
如图(a)所示,电子从加速电场的O点发出(初速不计),经电压为U1的加速电场加速后沿中心线进入两平行金属板M、N间的匀强电场中,通过电场后打到荧光屏上的P点处,设M、N板间的电压为U2,两极板间距离与板长相等,均为L1,板的右端到荧光屏的距离为L2,已知U1=200V,U2=300V,L1=6cm,L2=21cm,电子的比荷e/m=1.8×1011C/kg.求: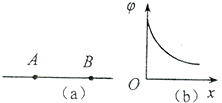 (2010?长春一模)如图(a)所示,AB是某电场中的一条电场线,若有一电子以某一初速度且仅在电场力的作用下,沿AB由点A运动到点B,所经位置的电势随距A点的距离变化的规律如图(b)所示.以下说法正确的是( )
(2010?长春一模)如图(a)所示,AB是某电场中的一条电场线,若有一电子以某一初速度且仅在电场力的作用下,沿AB由点A运动到点B,所经位置的电势随距A点的距离变化的规律如图(b)所示.以下说法正确的是( )