题目内容
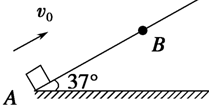 如图所示,m=1.0kg的小滑块以v0=4m/s的初速度从倾角为37°的斜面AB的底端A滑上斜面,滑块与斜面间的动摩擦因数为μ=0.5,取g=10m/s2,sin 37°=0.6.若从滑块滑上斜面起,经0.8s滑块正好通过B点,则AB之间的距离为( )
如图所示,m=1.0kg的小滑块以v0=4m/s的初速度从倾角为37°的斜面AB的底端A滑上斜面,滑块与斜面间的动摩擦因数为μ=0.5,取g=10m/s2,sin 37°=0.6.若从滑块滑上斜面起,经0.8s滑块正好通过B点,则AB之间的距离为( )分析:滑块向上运动时做匀减速直线运动,由牛顿第二定律求出滑块的加速度,由匀变速运动的速度位移公式与位移公式可以求出滑块的位移,最后求出AB间的距离.
解答:解:滑块向上滑行时,由牛顿第二定律得:
mgsin37°+μmgcos37°=ma,
解得:a=10m/s2,
滑块上滑,速度变为零需要的时间:t0=
=
=0.4s,
上滑的最大距离:s=
=
=0.8m,
经过0.4s,滑块达到最高点,速度为零,然后反向下滑,
由牛顿第二定律得:mgsin37°-μmgcos37°=ma′,
解得:a′=2m/s2,
下滑时间t′=t-t0=0.8s-0.4s,
下滑的距离s′=
a′t′2=
×2×0.42=0.16m,
AB间的 距离sAB=s-s′=0.8m-0.16m=0.64m;
故选:C.
mgsin37°+μmgcos37°=ma,
解得:a=10m/s2,
滑块上滑,速度变为零需要的时间:t0=
| v0 |
| g |
| 4 |
| 10 |
上滑的最大距离:s=
| ||
| 2a |
| 42 |
| 2×10 |
经过0.4s,滑块达到最高点,速度为零,然后反向下滑,
由牛顿第二定律得:mgsin37°-μmgcos37°=ma′,
解得:a′=2m/s2,
下滑时间t′=t-t0=0.8s-0.4s,
下滑的距离s′=
| 1 |
| 2 |
| 1 |
| 2 |
AB间的 距离sAB=s-s′=0.8m-0.16m=0.64m;
故选:C.
点评:分析清楚滑块的运动过程是正确解题的关键,应用牛顿第二定律与运动学公式即可正确解题;对于匀减速运动问题,要先求出其减速到零所用的时间.

练习册系列答案
相关题目

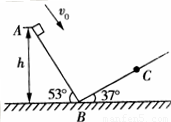
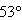 的斜面AB的顶点A滑下,不计滑过B点时的速度大小的变化,BC段斜面倾角为
的斜面AB的顶点A滑下,不计滑过B点时的速度大小的变化,BC段斜面倾角为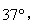 滑块与斜面间的动摩擦因数均为
滑块与斜面间的动摩擦因数均为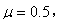 A点离B点所在水平面的高度h=1.2m。最大静摩擦力近似等于滑动摩擦力,取g=10m/s2,
A点离B点所在水平面的高度h=1.2m。最大静摩擦力近似等于滑动摩擦力,取g=10m/s2,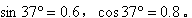
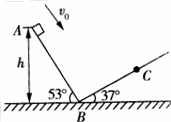
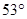 的斜面AB的顶点A滑下,不计滑过B点时的速度大小的变化,BC段斜面倾角为
的斜面AB的顶点A滑下,不计滑过B点时的速度大小的变化,BC段斜面倾角为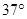 ,滑块与斜面间的动摩擦因数均为
,滑块与斜面间的动摩擦因数均为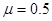 ,A点离B点所在水平面的高度h=1.2m。最大静摩擦力近似等于滑动摩擦力,取g=10m/s2,
,A点离B点所在水平面的高度h=1.2m。最大静摩擦力近似等于滑动摩擦力,取g=10m/s2,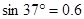 ,
,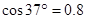 。
。
 =0.2,用水平推力F=20 N,使木块产生位移l1=3 m时撤去,木块又滑行l2=1 m时飞出平台,求木块落地时速度的大小?
=0.2,用水平推力F=20 N,使木块产生位移l1=3 m时撤去,木块又滑行l2=1 m时飞出平台,求木块落地时速度的大小?