题目内容
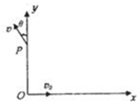 (2012?洛阳模拟)在如图所示的平面直角坐标系xoy中.有一个圆形区域的匀强磁场(图中未画出)磁场方向垂直于xoy平面,O点为该圆形区域边界上的一点.现有一质量为m,带电量为+q的带电粒子(重力不计)从O点开始以初速度vo沿+x方向进入磁场,粒子经过y轴上P点时速度方向与+y方向夹角为θ=30°,已知OP=L,求:
(2012?洛阳模拟)在如图所示的平面直角坐标系xoy中.有一个圆形区域的匀强磁场(图中未画出)磁场方向垂直于xoy平面,O点为该圆形区域边界上的一点.现有一质量为m,带电量为+q的带电粒子(重力不计)从O点开始以初速度vo沿+x方向进入磁场,粒子经过y轴上P点时速度方向与+y方向夹角为θ=30°,已知OP=L,求:(1)磁感应强度的大小和方向
(2)该圆形区域的最小面积.
分析:(1)根据左手定则判断磁场方向,画出运动轨迹,然后求解出轨道半径,最后根据洛伦兹力提供向心力列式求解;
(2)先求出连接粒子在磁场区入射点和出射点的弦长,要使圆形匀强磁场区域面积最小,其半径刚好为弦长的一半,求出半径即可求得面积.
(2)先求出连接粒子在磁场区入射点和出射点的弦长,要使圆形匀强磁场区域面积最小,其半径刚好为弦长的一半,求出半径即可求得面积.
解答:解:(1)由左手定则得磁场方向垂直xOy平面向里;
粒子在磁场中做弧长为
圆周的匀速圆周运动.如图所示.粒子在Q点飞出磁场,设其圆心为O′,半径为R,由几何关系有:
(L-R)sin30°=R
解得
R=
L
由牛顿第二定律得:qv0B=m
故:R=
由以上各式得磁感应强度:B=
(2)设磁场区的最小面积为S,由几何关系得
直径
-
R=
L
所以S=π(
)2=
L2
答:(1)磁感应强度的大小为
,方向垂直向内;
(2)该圆形区域的最小面积为
L2.
粒子在磁场中做弧长为
| 1 |
| 3 |
(L-R)sin30°=R
解得
R=
| 1 |
| 3 |
由牛顿第二定律得:qv0B=m
| ||
| R |
故:R=
| mv0 |
| qB |
由以上各式得磁感应强度:B=
| 3mv0 |
| qL |
(2)设磁场区的最小面积为S,由几何关系得
直径
. |
| OQ |
| 3 |
| ||
| 3 |
所以S=π(
| ||
| 2 |
| π |
| 12 |
答:(1)磁感应强度的大小为
| 3mv0 |
| qL |
(2)该圆形区域的最小面积为
| π |
| 12 |
点评:本题关键是画出轨迹后根据几何关系得到半径,然后根据洛伦兹力提供向心力求出磁感应强度,最后确定最小面积.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 (2012?洛阳模拟)如图所示,一个正电荷从x轴的c点分别沿直线被移动到y轴上的a点和b点,在这两个过程中,均需克服电场力做功,且做功的数值相同,有可能满足这种情况的电场是( )
(2012?洛阳模拟)如图所示,一个正电荷从x轴的c点分别沿直线被移动到y轴上的a点和b点,在这两个过程中,均需克服电场力做功,且做功的数值相同,有可能满足这种情况的电场是( ) (2012?洛阳模拟)一个质量为0.3kg的物体沿水平面做直线运动,如图所示,图线a表示物体受水平拉力时的v-t图象,图线b表示撤去水平拉力后物体继续运动的v-t图象,下列说法中正确的是( )
(2012?洛阳模拟)一个质量为0.3kg的物体沿水平面做直线运动,如图所示,图线a表示物体受水平拉力时的v-t图象,图线b表示撤去水平拉力后物体继续运动的v-t图象,下列说法中正确的是( ) (2012?洛阳模拟)一交流发电机的线圈电阻为1Ω,将其输出端接在电阻为10Ω的电阻丝上,其输出电压从某时刻开始随时间变化的图象如图所示,则( )
(2012?洛阳模拟)一交流发电机的线圈电阻为1Ω,将其输出端接在电阻为10Ω的电阻丝上,其输出电压从某时刻开始随时间变化的图象如图所示,则( )