题目内容
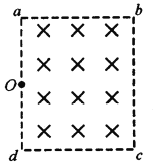
【题目】如图,边长ab=1.5L、bc=![]() L的矩形区域内存在着垂直于区域平面向里的匀强磁场,在ad边中点O处有一粒子源,可在区域平面内沿各方向发射速度大小相等的同种带电粒子。已知沿Od方向射入的粒子在磁场中运动的轨道半径为L,且经时间t0从边界cd离开磁场。不计粒子的重力和粒子间的相互作用,下列说法正确的是
L的矩形区域内存在着垂直于区域平面向里的匀强磁场,在ad边中点O处有一粒子源,可在区域平面内沿各方向发射速度大小相等的同种带电粒子。已知沿Od方向射入的粒子在磁场中运动的轨道半径为L,且经时间t0从边界cd离开磁场。不计粒子的重力和粒子间的相互作用,下列说法正确的是
A.粒子带负电
B.粒子可能从c点射出
C.粒子在磁场中做匀速圆周运动的周期为4t0
D.粒子在磁场中运动的最长时间为2t0
【答案】D
【解析】
粒子运动轨迹如下图所示:

A.根据左手定则可知粒子带正电,故A不符合题意;
B.当粒子轨迹与dc相切时,设切点与d点距离为x,由几何关系得:
![]()
解得:
![]()
则粒子不会达到c点,故B不符合题意;
C.设粒子轨迹对应的圆心角为![]() ,
,
![]()
解得:
![]()
根据题意得:
![]()
解得:
T=6t0
故C不符合题意;
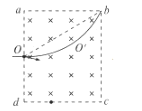
D.当有几何关系可以得到,粒子轨迹与bc边相切且从b点处射出时,在磁场中运动的时间最长,如下图所示:
![]()
设此时运动的角度为![]() ,由几何关系得:
,由几何关系得:
![]()
解得:
![]()
则运动时间为:
![]()
故D符合题意。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目