题目内容
8.用落体法验证机械能守恒定律的实验中,①运用公式$\frac{1}{2}$mv2=mgh对实验条件的要求是在打第一个点时,重锤恰好由静止开始下落,为此,所选择的纸带第1、2点间的距离应接近2mm.
②若实验中所用重锤的质量m=1kg,打点纸带如图所示(OA间有点未标出,O为起点),打点时间间隔为0.02s,则记录B点时,重锤的速度vB=0.59m/s,重锤的动能Ek=0.17J(保留小数点后两位),从开始下落起至B点重锤的重力势能的减小量是0.18J,(g取10m/s2,保留小数点后两位),由此可得出结论.

③根据纸带算出相关各点的速度v,量出下落的距离h,则以h为横轴画出的图象应是下图中的哪个C

分析 本题应从实验原理、纸带的选择、实验步骤、实验数据处理这几点去分析.
本实验是以自由落体运动为例来验证机械能守恒定律,纸带匀变速直线运动时,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度和加速度,从而求出动能.根据功能关系得重力势能减小量等于重力做功的数值.根据$\frac{{v}^{2}}{2}$-h的表达式,从数学的角度分析图象.
解答 解:①运用公式$\frac{1}{2}$mv2=mgh时,对纸带上起点的要求是重锤是从初速度为零开始.
打点计时器的打点频率为50 Hz,打点周期为0.02s,重物开始下落后,
由h=$\frac{1}{2}$gT2=×9.8×0.022 m≈2 mm得,
在第一个打点周期内重物下落的高度所以所选的纸带最初两点间的距离接近2mm.
②利用匀变速直线运动的推论vB=$\frac{{x}_{AC}}{2T}$=$\frac{0.0314-0.0078}{2×0.02}$m/s=0.59m/s,
重锤的动能EKB=$\frac{1}{2}$m${v}_{B}^{2}$=$\frac{1}{2}$×1×0.592J=0.17J
从开始下落至B点,重锤的重力势能减少量△Ep=mgh=1×10×0.176J=0.18J.
得出的结论是在误差允许范围内,重物下落的机械能守恒.
③物体自由下落过程中,由机械能守恒可以得出:
mgh=$\frac{1}{2}$mv2,即$\frac{1}{2}$v2=gh
所以以$\frac{1}{2}$v2为纵轴,以h为横轴画出的图线应是过原点的倾斜直线,也就是图中的C.
故选:C.
故答案为:①在打第一个点时,重锤恰好由静止开始下落,2mm;
②0.59m/s,0.17J,0.18J;③C.
点评 本题关键从实验原理出发,分析纸带的选择,数据处理,并能得出结论.利用图象问题结合数学知识处理物理数据是实验研究常用的方法.我们更多的研究直线图形,找出其直线的斜率和截距.

 将横截面积为S的玻璃管弯成如图所示的连通器,放在水平桌面上,左、右管处在竖直状态,先关闭阀门K,往左、右管中分别注入高度为h2、h1,密度为ρ的液体,然后打开阀门K,直到液体静止,重力对液体做的功为( )
将横截面积为S的玻璃管弯成如图所示的连通器,放在水平桌面上,左、右管处在竖直状态,先关闭阀门K,往左、右管中分别注入高度为h2、h1,密度为ρ的液体,然后打开阀门K,直到液体静止,重力对液体做的功为( )| A. | ρgs(h2-h1) | B. | $\frac{1}{4}$ρgs(h2-h1) | C. | $\frac{1}{4}$ρgs(h2-h1)2 | D. | $\frac{1}{2}$ρgs(h2-h1)2 |
 在如图所示的电路中,电源的负极接地,其电动势为E、内电阻为r,R1、R2为定值电阻,R3为滑动变阻器,C为电容器,A、V为理想电流表和理想电压表.在滑动变阻器滑动头P自a端向b端滑动的过程中,下列说法中正确的是( )
在如图所示的电路中,电源的负极接地,其电动势为E、内电阻为r,R1、R2为定值电阻,R3为滑动变阻器,C为电容器,A、V为理想电流表和理想电压表.在滑动变阻器滑动头P自a端向b端滑动的过程中,下列说法中正确的是( )| A. | 电压表示数变小 | B. | 电流表示数变小 | ||
| C. | a点的电势升高 | D. | 电容器C所带电荷量减少 |

| A. | 在0~6s内,物体离出发点最远为30m | |
| B. | 在0~6s内,物体经过的路程为50m | |
| C. | 在0~6s内,物体的平均速度为5m/s | |
| D. | 在4~6s内,物体的加速度的方向发生了变化 |
| A. | 换用缝距大些的双缝片 | B. | 换用缝距小些的双缝片 | ||
| C. | 适当调大双缝与屏的距离 | D. | 适当调小双缝与屏的距离 |

| A. | 图甲,感应电动势不为零且恒定不变 | |
| B. | 图乙,感应电动势一直增大 | |
| C. | 图丙,0~t1时间内的感应电动势小于t1~t2时间内的感应电动势 | |
| D. | 图丁,感应电动势先变小再变大 |
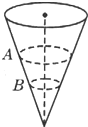 如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则( )
如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则( )| A. | 球A的线速度必定小于球B的线速度 | |
| B. | 球A的角速度必定大于球B的角速度 | |
| C. | 球A的运动周期必定小于球B的运动周期 | |
| D. | 球A对筒壁的压力必定等于球B对筒壁的压力 |
 如图所示,R1为定值电阻,R2为最大阻值为2R1的可变电阻.E为电源电动势,r为电源内阻,大小为r=R1.当R2的滑动臂P从a滑向b的过程中,下列说法正确的是( )
如图所示,R1为定值电阻,R2为最大阻值为2R1的可变电阻.E为电源电动势,r为电源内阻,大小为r=R1.当R2的滑动臂P从a滑向b的过程中,下列说法正确的是( )| A. | 电阻R2的功率先增大后减小 | |
| B. | 电源的输出功率先增大后减小 | |
| C. | 电压表示数和电流表示数之比逐渐增大 | |
| D. | 电压表示数的变化量和电流表示数的变化量之比逐渐增大 |
 质量为1kg的质点在x-y平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图所示.下列说法正确的是( )
质量为1kg的质点在x-y平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图所示.下列说法正确的是( )| A. | 质点的初速度为5 m/s | B. | 质点所受的合外力为3N | ||
| C. | 质点做类平抛运动 | D. | 2s末质点速度大小为6m/s |