题目内容
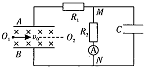
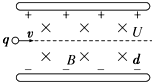
汤姆生曾采用电场、磁场偏转法测定电子的比荷，具体方法如下：
Ⅰ．使电子以初速度v1垂直通过宽为L的匀强电场区域，测出偏向角θ，已知匀强电场的场强大小为E，方向如图（a）所示
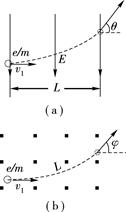
Ⅱ．使电子以同样的速度v1垂直射入磁感应强度大小为B、方向如图（b）所示的匀强磁场，使它刚好经过路程长度为L的圆弧之后射出磁场，测出偏向角φ，请继续完成以下三个问题：
（1）电子通过匀强电场和匀强磁场的时间分别为多少？
（2）若结果不用v1表达，那么电子在匀强磁场中做圆弧运动对应的圆半径R为多少？
（3）若结果不用v1表达，那么电子的比荷e / m为多少？
Ⅰ．使电子以初速度v1垂直通过宽为L的匀强电场区域，测出偏向角θ，已知匀强电场的场强大小为E，方向如图（a）所示
Ⅱ．使电子以同样的速度v1垂直射入磁感应强度大小为B、方向如图（b）所示的匀强磁场，使它刚好经过路程长度为L的圆弧之后射出磁场，测出偏向角φ，请继续完成以下三个问题：
（1）电子通过匀强电场和匀强磁场的时间分别为多少？
（2）若结果不用v1表达，那么电子在匀强磁场中做圆弧运动对应的圆半径R为多少？
（3）若结果不用v1表达，那么电子的比荷e / m为多少？
（1）t=L/v1；（2）R=L/φ；（3）e/m=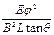
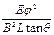
（1）电子通过匀强电场和匀强磁场的时间相等，分别都是：t=L/v1…………①（2分）
（2）电子进入匀强磁场中作匀速圆周运动有：R=L/φ…………………… ②（2分）
（3）沿电场力方向有：vy=at=eEL/mv1………………………………………③（1分）
电子射出电场时的速度偏向角满足：tanθ=vy/v1…………………………④（1分）
由牛顿第二定律，有：e v1B =" m"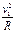
………………………………………⑤（1分）
综合②③④⑤，解得：e/m=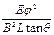………………………………………………⑥（2分
（2）电子进入匀强磁场中作匀速圆周运动有：R=L/φ…………………… ②（2分）
（3）沿电场力方向有：vy=at=eEL/mv1………………………………………③（1分）
电子射出电场时的速度偏向角满足：tanθ=vy/v1…………………………④（1分）
由牛顿第二定律，有：e v1B =" m"
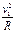………………………………………⑤（1分）综合②③④⑤，解得：e/m=
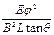………………………………………………⑥（2分
练习册系列答案
相关题目
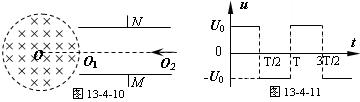
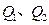，杆上套着一带正电小球，整个装置处在一个匀强磁场中，磁感应强度方向垂直纸面向里，将靠近右端的小球从静止开始释放，在小球从右到左的运动过程中，下列说法正确的是（）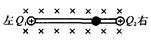
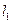和
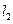的两个毗邻的条形区域分别有匀强磁场和匀强电场，磁场方向垂直于纸面向里，电场方向与电、磁场分界线平行向右。一带正电荷的粒子以速率v从磁场区域上边界的P点斜射入磁场，然后以垂直于电、磁场分界线的方向进入电场，最后从电场边界上的Q点射出。已知PQ垂直于电场方向，粒子轨迹与电、磁场分界线的交点到PQ的距离为d。不计重力,求电场强度与磁感应强度大小之比及粒子在磁场与电场中运动时间之比。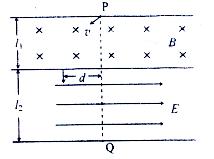
间，匀强磁场的方向垂直纸面向外，电场方向水平向右，滑块与木板之间的摩擦系数为μ．已知滑块由P点沿木板做匀速直线运动到Q点与开关碰撞，将Q点的开关撞开，使电场消失，只保留磁场，离开开关时滑块的动能变为原来的
