题目内容
特种兵过山谷的一种方法可化简为如右图所示的模型:将一根长为2d、不可伸长的细绳的两端固定在相距为d的A、B两等高处,悬绳上有小滑轮P,战士们相互配合,可沿着细绳滑到对面。开始时,战士甲拉住滑轮,质量为m的战士乙吊在滑轮上,处于静止状态,AP竖直,则此时甲对滑轮的水平拉力为_________mg;若甲将滑轮由静止释放,则乙在滑动中速度的最大值为_________。(不计滑轮与绳的质量,不计滑轮的大小及摩擦) 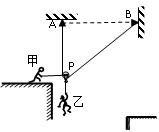
1/2 
解析试题分析:设开始位置绳子的拉力为T,PB与竖直线的夹角为α,则对滑轮,水平方向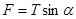 ,竖直方向
,竖直方向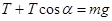 ,由几何关系
,由几何关系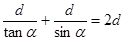 ,化简得2sinα=cosα+1.所以F=mg/2。若设AP=x,则x2+d2=(2d-x)2,解得x=3d/4.当滑轮滑到最低点时,速度最大,在最低点时滑轮距离A点的竖直距离为
,化简得2sinα=cosα+1.所以F=mg/2。若设AP=x,则x2+d2=(2d-x)2,解得x=3d/4.当滑轮滑到最低点时,速度最大,在最低点时滑轮距离A点的竖直距离为 ,由机械能守恒定律mg(
,由机械能守恒定律mg(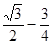 )d=
)d= ,解得v=
,解得v= .
.
考点:此题考查共点力的平衡、正交分解法及动能定理。

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
两个共点力F1、F2大小不同,它们的合力大小为F,则
| A.F1、F2同时增大一倍,F也增大一倍 |
| B.F1、F2同时增加10 N,F也增加10 N |
| C.F1增加10 N,F2减少10 N,F一定不变 |
| D.若F1、F2中的一个增大,F不一定增大 |
两倾斜的滑杆上分别套有A、B两个圆环,两圆环上分别用细线悬吊着一个物体,如右图所示.当它们都沿滑杆向下滑动时,A的悬线与滑杆垂直,B的悬线竖直向下,则( )
| A.A圆环与滑杆有摩擦力 |
| B.B圆环与滑杆无摩擦力 |
| C.A圆环做的是匀速运动 |
| D.B圆环做的是匀速运动 |



 ,重力加速度g取10 m/s2.求:
,重力加速度g取10 m/s2.求:

 ),静止在水平面上,当将一质量为m的木块放在斜面上时正好匀速下滑.如果用与斜面成α角的力F拉着木块匀速上滑(木块匀速上滑过程木楔仍在水平面上静止),如图所示,
),静止在水平面上,当将一质量为m的木块放在斜面上时正好匀速下滑.如果用与斜面成α角的力F拉着木块匀速上滑(木块匀速上滑过程木楔仍在水平面上静止),如图所示,