题目内容
将小球A以初速度vA=40m/s从地面上一点竖直向上抛出,经过一段时间△t后又以初速度vB=30m/s将球B从同一点竖直向上抛出,为了使两球能在空中相遇,试分析△t应满足什么条件.
【答案】分析:首先根据匀变速直线运动的速度时间关系式解出两球落地所需的时间,为了使两球能在空中相遇,我们可以在A球就要落回地面时才抛出B球,则B球会在地面上方与A球迎面相碰;也可以B球抛出后快回到地面时,被A球追上相碰;根据两种极限情况列式求解.
解答:解:设A、B两球在空中运动的时间分别为tA、tB,
由竖直上抛运动的速度时间关系式
可得: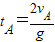 =8s,
=8s,
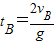 =6s
=6s
考虑△t的上限,即A球就要落回地面时才抛出B球,则B球会在地面上方与A球迎面相碰,
故应有:△t<tA
考虑△t的下限,即B球抛出后快回到地面时,被A球追上相碰,
故应由:△t>tA-tB
由题中数据vA=40m/s,vB=30m/s
即可得:2s<△t<8s
答:当△t应满足2s<△t<8s条件时,两球能在空中相遇.
点评:两个球的竖直上抛问题,实际上可以看成是追及问题.可以把他们当成追 及问题来处理,追及问题的处理方法.找三个关系:时间关系,位置关系,速度关系,再列方程.
解答:解:设A、B两球在空中运动的时间分别为tA、tB,
由竖直上抛运动的速度时间关系式
可得:
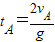 =8s,
=8s,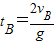 =6s
=6s考虑△t的上限,即A球就要落回地面时才抛出B球,则B球会在地面上方与A球迎面相碰,
故应有:△t<tA
考虑△t的下限,即B球抛出后快回到地面时,被A球追上相碰,
故应由:△t>tA-tB
由题中数据vA=40m/s,vB=30m/s
即可得:2s<△t<8s
答:当△t应满足2s<△t<8s条件时,两球能在空中相遇.
点评:两个球的竖直上抛问题,实际上可以看成是追及问题.可以把他们当成追 及问题来处理,追及问题的处理方法.找三个关系:时间关系,位置关系,速度关系,再列方程.

练习册系列答案
相关题目