题目内容
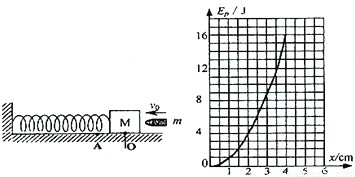 弹簧在不受作用力时所具有的长度称为自然长度,记为l;弹簧受到拉力作用后会伸长,受到压力作用后会缩短,如果受力作用时的长度称为实际长度,记为l;而l与l之差的绝对值称为形变量,记为x;x=|l-l|.有一弹簧振子如图所示,放在光滑的水平面上,弹簧处于自然长度时M静止在O位置,一质量为m=20g的子弹,以一定的初速度v射入质量为M=1980g的物块中,并留在其中一起压缩弹簧.振子在振动的整个过程中,弹簧的弹性势能随弹簧的形变量变化的关系如图所示.则:
弹簧在不受作用力时所具有的长度称为自然长度,记为l;弹簧受到拉力作用后会伸长,受到压力作用后会缩短,如果受力作用时的长度称为实际长度,记为l;而l与l之差的绝对值称为形变量,记为x;x=|l-l|.有一弹簧振子如图所示,放在光滑的水平面上,弹簧处于自然长度时M静止在O位置,一质量为m=20g的子弹,以一定的初速度v射入质量为M=1980g的物块中,并留在其中一起压缩弹簧.振子在振动的整个过程中,弹簧的弹性势能随弹簧的形变量变化的关系如图所示.则:(1)根据图线可以看出,M被子弹击中后将在O点附近哪一区间运动?
(2)子弹的初速度v为多大?
(3)当M运动到O点左边离O点2cm的A点处时,速度u多大?
(4)现若水平面粗糙,上述子弹击中M后同样从O点运动到A点时,振子的速度变为3m/s,则M从开始运动到运动到A点的过程中,地面的摩擦力对M做了多少功?弹簧的弹力对M做了多少功?
【答案】分析:(1)从图中可以看出当x=4cm时,弹簧的弹性势能最大,此时速度为0,即可求得M被子弹击中后将在O点附近哪一区间运动;
(2)子弹和物块一起压缩弹簧的过程中系统机械能守恒,求出刚射入时的共同速度,子弹射入物块时间极短,瞬间子弹、物块组成的系统动量守恒,根据动量守恒即可求解;
(3)从图线可以看出:M运动到O点左边2cm处时的弹性势力能为EP=4J,子弹和物块一起压缩弹簧的过程中根据系统机械能守恒求出速度;
(4)根据功能关系及动能定理即可求解.
解答:解:(1)从图中可以看出当x=4cm时,弹簧的弹性势能最大,此时速度为0,所以O点的左边4cm-O点的右边4cm的范围内运动.
(2)子弹和物块一起压缩弹簧的过程中系统机械能守恒,故系统的机械能为Ekm=Epm=16J
则可求出子弹射入物块后两者的共同速度v为: ,v=4 m/s
,v=4 m/s
子弹射入物块时间极短,瞬间子弹、物块组成的系统动量守恒,则mv=(m+M)v
v=400 m/s
(3)从图线可以看出:M运动到O点左边2cm处时,形变量x=2 cm,此时弹性势力能为EP=4J,子弹和物块一起压缩弹簧的过程中系统机械能守恒,
故有:Ekm=Epm=Ek+EP,
解得:u=2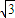 m/s
m/s
(4)设地面的摩擦力对M做的功记为Wf,M从开始运动到A点,根据功和能的关系有: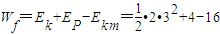 =-3J
=-3J
设弹簧的弹力对M做的功记为Wk,M从开始运动到A点,根据动能定理有: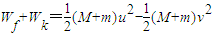 ,Wk=-4J
,Wk=-4J
答:(1)根据图线可以看出,M被子弹击中后将在O点的左边4cm至O点的右边4cm的范围内运动;
(2)子弹的初速度v为400 m/s;
(3)当M运动到O点左边离O点2cm的A点处时,速度u为2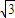 m/s;
m/s;
(4)地面的摩擦力对M做的功为-3J,弹簧的弹力对M做的功为-4J.
点评:本题主要考查了机械能守恒定律、动量守恒定律及动能定理的应用,能根据图象得出有效信息,难度适中.
(2)子弹和物块一起压缩弹簧的过程中系统机械能守恒,求出刚射入时的共同速度,子弹射入物块时间极短,瞬间子弹、物块组成的系统动量守恒,根据动量守恒即可求解;
(3)从图线可以看出:M运动到O点左边2cm处时的弹性势力能为EP=4J,子弹和物块一起压缩弹簧的过程中根据系统机械能守恒求出速度;
(4)根据功能关系及动能定理即可求解.
解答:解:(1)从图中可以看出当x=4cm时,弹簧的弹性势能最大,此时速度为0,所以O点的左边4cm-O点的右边4cm的范围内运动.
(2)子弹和物块一起压缩弹簧的过程中系统机械能守恒,故系统的机械能为Ekm=Epm=16J
则可求出子弹射入物块后两者的共同速度v为:
 ,v=4 m/s
,v=4 m/s子弹射入物块时间极短,瞬间子弹、物块组成的系统动量守恒,则mv=(m+M)v
v=400 m/s
(3)从图线可以看出:M运动到O点左边2cm处时,形变量x=2 cm,此时弹性势力能为EP=4J,子弹和物块一起压缩弹簧的过程中系统机械能守恒,
故有:Ekm=Epm=Ek+EP,
解得:u=2
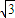 m/s
m/s(4)设地面的摩擦力对M做的功记为Wf,M从开始运动到A点,根据功和能的关系有:
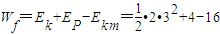 =-3J
=-3J设弹簧的弹力对M做的功记为Wk,M从开始运动到A点,根据动能定理有:
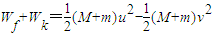 ,Wk=-4J
,Wk=-4J答:(1)根据图线可以看出,M被子弹击中后将在O点的左边4cm至O点的右边4cm的范围内运动;
(2)子弹的初速度v为400 m/s;
(3)当M运动到O点左边离O点2cm的A点处时,速度u为2
 m/s;
m/s;(4)地面的摩擦力对M做的功为-3J,弹簧的弹力对M做的功为-4J.
点评:本题主要考查了机械能守恒定律、动量守恒定律及动能定理的应用,能根据图象得出有效信息,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2008?广东模拟)弹簧在不受作用力时所具有的长度称为自然长度,记为l0;弹簧受到拉力作用后会伸长,受到压力作用后会缩短,如果受力作用时的长度称为实际长度,记为l;而l与l0之差的绝对值称为形变量,记为x;x=|l-l0|.有一弹簧振子如图所示,放在光滑的水平面上,弹簧处于自然长度时M静止在O位置,一质量为m=20g的子弹,以一定的初速度v0射入质量为M=1980g的物块中,并留在其中一起压缩弹簧.振子在振动的整个过程中,弹簧的弹性势能随弹簧的形变量变化的关系如图所示.则:
(2008?广东模拟)弹簧在不受作用力时所具有的长度称为自然长度,记为l0;弹簧受到拉力作用后会伸长,受到压力作用后会缩短,如果受力作用时的长度称为实际长度,记为l;而l与l0之差的绝对值称为形变量,记为x;x=|l-l0|.有一弹簧振子如图所示,放在光滑的水平面上,弹簧处于自然长度时M静止在O位置,一质量为m=20g的子弹,以一定的初速度v0射入质量为M=1980g的物块中,并留在其中一起压缩弹簧.振子在振动的整个过程中,弹簧的弹性势能随弹簧的形变量变化的关系如图所示.则: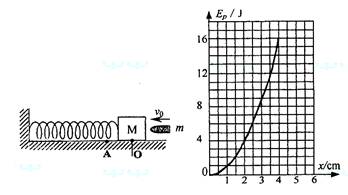 (4)现若水平面粗糙,上述子弹击中M后同样从O点运动到A点时,振子的速度变为3 m/s,则M从开始运动到A点的过程中,地面的摩擦力对M做了多少功?弹簧的弹力对M做了多少功?
(4)现若水平面粗糙,上述子弹击中M后同样从O点运动到A点时,振子的速度变为3 m/s,则M从开始运动到A点的过程中,地面的摩擦力对M做了多少功?弹簧的弹力对M做了多少功?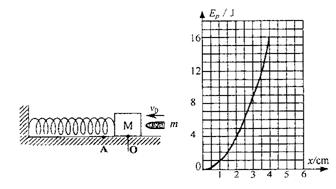 (4)现若水平面粗糙,上述子弹击中M后同样从O点运动到A点时,振子的速度变为3m/s,则M从开始运动到运动到A点的过程中,地面的摩擦力对M做了多少功?弹簧的弹力对M做了多少功?
(4)现若水平面粗糙,上述子弹击中M后同样从O点运动到A点时,振子的速度变为3m/s,则M从开始运动到运动到A点的过程中,地面的摩擦力对M做了多少功?弹簧的弹力对M做了多少功?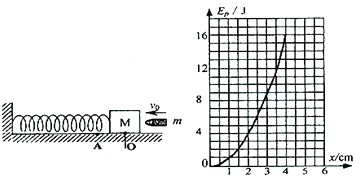
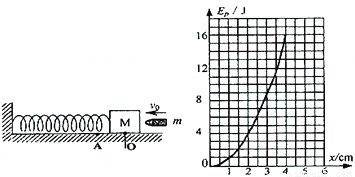 弹簧在不受作用力时所具有的长度称为自然长度,记为l;弹簧受到拉力作用后会伸长,受到压力作用后会缩短,如果受力作用时的长度称为实际长度,记为l;而l与l之差的绝对值称为形变量,记为x;x=|l-l|.有一弹簧振子如图所示,放在光滑的水平面上,弹簧处于自然长度时M静止在O位置,一质量为m=20g的子弹,以一定的初速度v射入质量为M=1980g的物块中,并留在其中一起压缩弹簧.振子在振动的整个过程中,弹簧的弹性势能随弹簧的形变量变化的关系如图所示.则:
弹簧在不受作用力时所具有的长度称为自然长度,记为l;弹簧受到拉力作用后会伸长,受到压力作用后会缩短,如果受力作用时的长度称为实际长度,记为l;而l与l之差的绝对值称为形变量,记为x;x=|l-l|.有一弹簧振子如图所示,放在光滑的水平面上,弹簧处于自然长度时M静止在O位置,一质量为m=20g的子弹,以一定的初速度v射入质量为M=1980g的物块中,并留在其中一起压缩弹簧.振子在振动的整个过程中,弹簧的弹性势能随弹簧的形变量变化的关系如图所示.则: