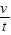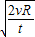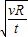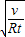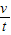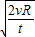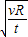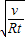Question

某人站在一星球上，以速度v₀竖直向上抛一小球，经t秒后，球落回手中，已知该星球半径为R，现将此球沿此星球表面将小球水平抛出，欲使其不落回星球，则抛出时的速度至少为（　　）

• A．

  v0

  t

• B．

  2v0R t

• C．

  v0R t

• D．

  v0 Rt

Answer 1

分析：（1）可由竖直上抛运动的初速度和时间求出星球表面的重力加速度．
（2）现将此球沿此星球表面将小球水平抛出，欲使其不落回星球，则抛出时的速度至少为该星球第一宇宙速度

GM R

=

gR

求解．

解答：解：设该星球表面的引力加速度为：g'，则上升到最高点用的时间t'为：
t'=

v0

g’

所以落回手中用时为：
2t'=

2v0

g’

=t
所以：g'=

2v0

t

现将此球沿此星球表面将小球水平抛出，欲使其不落回星球，则抛出时的速度至少为该星球的第一宇宙速度：
所以：v=

g’R

=

2v0R t

故选：B

点评：此题本质是求第一宇宙速度，计算第一宇宙速度时需要求解星球表面的重力加速度，这个加速度可由自由落体运动，竖直上抛运动，平抛运动，单摆周期等知识求出．