题目内容
放在水平地面上的一物块,受到方向不变的水平推力F的作用,F的大小与时间t的关系如图1所示和物块速度v与时间t 的关系如图2所示.
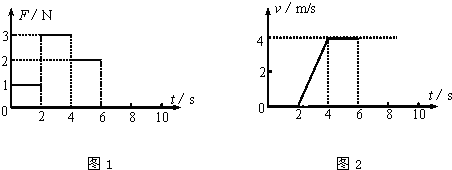
求:(1)物块的质量m;
(2)物块与地面之间的动摩擦因数μ;
(3)撤去拉力后物体还能滑行多远.
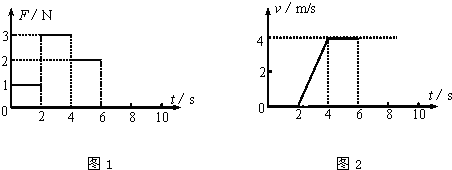
求:(1)物块的质量m;
(2)物块与地面之间的动摩擦因数μ;
(3)撤去拉力后物体还能滑行多远.
分析:(1)由v-t图象看出,物体在4-6s做匀速运动,由F-t图象读出物块在运动过程中受到的滑动摩擦力;由v-t图象的斜率求出物体在2-4s物体的加速度,根据牛顿第二定律求出物体的质量m.
(2)根据滑动摩擦力公式求出动摩擦因数μ.
(3)撤去推力后,物体由于惯性继续运动,根据动能定理列式求解还能滑行多远.
(2)根据滑动摩擦力公式求出动摩擦因数μ.
(3)撤去推力后,物体由于惯性继续运动,根据动能定理列式求解还能滑行多远.
解答:解:(1)由v-t图象看出,物体在4s-6s做匀速直线运动,则f=F3=2N
由速度图象可知,2-4s物体加速度为:
a=
=
=
=2m/s2,F=3N
由牛顿第二定律得:F-f=ma
代入解得:m=0.5kg
(2)由f=μN=μmg
得:μ=
=
=0.4
(3)撤去推力后,物体由于惯性继续运动,根据动能定理,有:
-fx=0-
mv2
解得:x=
=
=2m
答:(1)物块的质量0.5kg;
(2)物块与地面之间的动摩擦因数0.4;
(3)撤去拉力后物体还能滑行2m.
由速度图象可知,2-4s物体加速度为:
a=
| △v |
| △t |
| v-v0 |
| t |
| 4-0 |
| 4-2 |
由牛顿第二定律得:F-f=ma
代入解得:m=0.5kg
(2)由f=μN=μmg
得:μ=
| f |
| mg |
| 2 |
| 5 |
(3)撤去推力后,物体由于惯性继续运动,根据动能定理,有:
-fx=0-
| 1 |
| 2 |
解得:x=
| mv2 |
| 2f |
| 0.5×42 |
| 2×2 |
答:(1)物块的质量0.5kg;
(2)物块与地面之间的动摩擦因数0.4;
(3)撤去拉力后物体还能滑行2m.
点评:本题一方面考查读图能力,由速度图线的斜率求出加速度;另一方面要能由加速度应用牛顿运动定律求出质量;最后还要能根据受力情况确定运动情况.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 (2008?滨州一模)放在水平地面上的一物块,受到方向不变的水平推力F的作用,力F的大小与时间t的关系和物块速度v与时间t的关系如图所示.重力加速度g=10m/s2.求:
(2008?滨州一模)放在水平地面上的一物块,受到方向不变的水平推力F的作用,力F的大小与时间t的关系和物块速度v与时间t的关系如图所示.重力加速度g=10m/s2.求: 放在水平地面上的一物块,受到方向不变的水平推力F的作用,力F的大小与时间t的关系和物块速度v与时间t的部分关系如图所示,重力加速度g=10m/s2,求:
放在水平地面上的一物块,受到方向不变的水平推力F的作用,力F的大小与时间t的关系和物块速度v与时间t的部分关系如图所示,重力加速度g=10m/s2,求: 放在水平地面上的一物块,受到方向不变的水平推力F的作用,F的大小与时间t的关系和物块速度v与时间t 的关系如图所示.取重力加速度g=10m/s2.求:
放在水平地面上的一物块,受到方向不变的水平推力F的作用,F的大小与时间t的关系和物块速度v与时间t 的关系如图所示.取重力加速度g=10m/s2.求: 放在水平地面上的一物块,受到方向不变的水平推力F的作用,力F的大小与时间t的关系和物块速度v与时间t的关系如图所示,重力加速度g=10m/s2,求:
放在水平地面上的一物块,受到方向不变的水平推力F的作用,力F的大小与时间t的关系和物块速度v与时间t的关系如图所示,重力加速度g=10m/s2,求: 放在水平地面上的一物块,受到方向不变的水平推力F的作用,力F的大小与时间t的关系和物块速度v与时间t的关系如图所示.取重力加速度g=10m/s2.试利用两图线求:
放在水平地面上的一物块,受到方向不变的水平推力F的作用,力F的大小与时间t的关系和物块速度v与时间t的关系如图所示.取重力加速度g=10m/s2.试利用两图线求: