题目内容
15. 如图甲,一质量为M、横截面积为S的光滑活塞静止时密封一定量的理想气体,此时活塞距气缸底部距离为H.现将气缸倒转悬挂(活塞不脱离气缸)如图乙,求活塞平衡时到缸底的距离.(已知大气压强为P0.)
如图甲,一质量为M、横截面积为S的光滑活塞静止时密封一定量的理想气体,此时活塞距气缸底部距离为H.现将气缸倒转悬挂(活塞不脱离气缸)如图乙,求活塞平衡时到缸底的距离.(已知大气压强为P0.)
分析 对活塞受力分析,根据平衡条件求出开始时气体的压强;气缸倒置后,对活塞受力分析根据平衡条件列出等式求出气体的压强,然后对封闭气体运用玻意耳定律求解.
解答 解:开口向上时,对活塞受力分析:
Mg+P0S=P1S
得:P=$\frac{Mg{+P}_{0}S}{S}$
气缸倒置后:
对活塞受力分析得:Mg+P2S=P0S
所以P2=$\frac{{P}_{0}S-Mg}{S}$
对封闭气体运用玻意耳定律,得:P1HS=P2H2S
联立解得:H2=$\frac{{P}_{0}S+Mg}{{P}_{0}S-Mg}•H$
答:活塞平衡时到缸底的距离是$\frac{{P}_{0}S+Mg}{{P}_{0}S-Mg}•H$.
点评 该题结合封闭气体的压强的求法,考查理想气体的状态方程,解答的关键要能对活塞受力分析,能根据平衡条件求出气体的压强的表达式.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
6.可视为质点的甲、乙两物体相距一定距离,当质量分别为m和5m时万有引力为F.若仅将甲物体质量增为2m,乙物体质量减为3m时,万有引力将( )
| A. | 大于F | B. | 等于F | C. | 小于F | D. | 不能判断 |
10.某空间站正在地球赤道平面内的圆周轨道上运行,其离地球表面的高度为同步卫星离地球表面高度的十分之一,且运行方向与地球自转方向一致.下列说法正确的是( )
| A. | 空间站运行的加速度小于地球表面的重力加速度 | |
| B. | 站在地球赤道上的人观察到空间站向东运动 | |
| C. | 在空间站工作的宇航员因受到平衡力作用而在舱中悬浮或静止 | |
| D. | 空间站运行的速度大于同步卫星运行速度 |
20.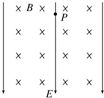 如图所示,空间存在相互垂直的匀强电场和匀强磁场,电场的方向竖直向下,磁场方向水平(图中垂直纸面向里),一带电油滴P恰好处于静止状态,则下列说法正确的是( )
如图所示,空间存在相互垂直的匀强电场和匀强磁场,电场的方向竖直向下,磁场方向水平(图中垂直纸面向里),一带电油滴P恰好处于静止状态,则下列说法正确的是( )
 如图所示,空间存在相互垂直的匀强电场和匀强磁场,电场的方向竖直向下,磁场方向水平(图中垂直纸面向里),一带电油滴P恰好处于静止状态,则下列说法正确的是( )
如图所示,空间存在相互垂直的匀强电场和匀强磁场,电场的方向竖直向下,磁场方向水平(图中垂直纸面向里),一带电油滴P恰好处于静止状态,则下列说法正确的是( )| A. | 若仅撤去电场,P可能做匀加速直线运动 | |
| B. | 若仅撤去磁场,P一定做匀速直线运动 | |
| C. | 若给P一初速度,P不可能做匀速直线运动 | |
| D. | 若给P一初速度,P可能做匀速圆周运动 |
5.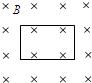 如图所示,闭合金属线圈置于匀强磁场中,线圈平面与磁场方向垂直.保持磁场的方向不变,下列各种操作中,线圈各边均未离开磁场.则能使线圈内产生感应电流的是( )
如图所示,闭合金属线圈置于匀强磁场中,线圈平面与磁场方向垂直.保持磁场的方向不变,下列各种操作中,线圈各边均未离开磁场.则能使线圈内产生感应电流的是( )
 如图所示,闭合金属线圈置于匀强磁场中,线圈平面与磁场方向垂直.保持磁场的方向不变,下列各种操作中,线圈各边均未离开磁场.则能使线圈内产生感应电流的是( )
如图所示,闭合金属线圈置于匀强磁场中,线圈平面与磁场方向垂直.保持磁场的方向不变,下列各种操作中,线圈各边均未离开磁场.则能使线圈内产生感应电流的是( )| A. | 将线圈平行纸面向上移动 | B. | 将线圈平行纸面向右移动 | ||
| C. | 将线圈垂直纸面向外拉动 | D. | 将线圈以某一边为轴转动 |
 如图所示,在光滑的水平桌面上有一金属容器C,其质量为mC=5kg,在C的中央并排放着两个可视为质点的滑块A与B,其质量分别为mA=1kg、mB=4kg.开始时A、B、C均处于静止状态,用细线拉紧A、B使其中间夹有的轻弹簧处于压缩状态,剪断细线,使得A以vA=6m/s的速度水平向左弹出,不计一切摩擦,两滑块中任意一个与C侧壁碰撞后就与其合成一体,求:
如图所示,在光滑的水平桌面上有一金属容器C,其质量为mC=5kg,在C的中央并排放着两个可视为质点的滑块A与B,其质量分别为mA=1kg、mB=4kg.开始时A、B、C均处于静止状态,用细线拉紧A、B使其中间夹有的轻弹簧处于压缩状态,剪断细线,使得A以vA=6m/s的速度水平向左弹出,不计一切摩擦,两滑块中任意一个与C侧壁碰撞后就与其合成一体,求: 如图所示,光滑水平面右端B处连接一个竖直的半径为R的半圆形轨道,在与B距离为x的A点,用水平恒力F将质量为m的小球从静止开始推到B处后撤去该恒力,小球沿半圆轨道运动到C处后又正好落回A点,求:
如图所示,光滑水平面右端B处连接一个竖直的半径为R的半圆形轨道,在与B距离为x的A点,用水平恒力F将质量为m的小球从静止开始推到B处后撤去该恒力,小球沿半圆轨道运动到C处后又正好落回A点,求:
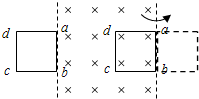 如图所示,空间存在竖直向下的有界匀强磁场B,一单匝边长为L,质量为m的正方形线框abcd放在水平桌面上,在水平外力作用下从左边界以速度v匀速进入磁场,当cd边刚好进入磁场后立刻撤去外力,线框ab边恰好能到达磁场的右边界,然后将线框以ab边为轴,以角速度ω匀速翻转到图示虚线位置.已知线框与桌面间动摩擦因数为μ,磁场宽度大于L,线框电阻为R,重力加速度为g,求:
如图所示,空间存在竖直向下的有界匀强磁场B,一单匝边长为L,质量为m的正方形线框abcd放在水平桌面上,在水平外力作用下从左边界以速度v匀速进入磁场,当cd边刚好进入磁场后立刻撤去外力,线框ab边恰好能到达磁场的右边界,然后将线框以ab边为轴,以角速度ω匀速翻转到图示虚线位置.已知线框与桌面间动摩擦因数为μ,磁场宽度大于L,线框电阻为R,重力加速度为g,求: