题目内容
图中AB是光滑斜面轨道，AEB、ACD是光滑的折面轨道，但在C、E处都有光滑的圆弧过渡，ACD的总长度等于AB，现让一个小球先后三次在不同的轨道上自最高处A无初速释放，到小球接触水平面为止，则（ ）
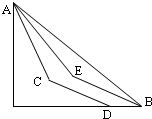
| A．沿ACD线用时最短 |
| B．沿AEB线用时最长 |
| C．沿AEB线用时比沿AB线用时短 |
| D．沿ACD线用时与沿AB线用时一样长 |
根据动能定理得，mgh=
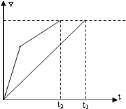
mv2，则到达底端的速率相等．比较ACD段和AB段，作速度时间图线，因为路程相等，则图线与时间轴所围成的面积相等．如图，沿AB段运动的时间为t1，沿ACD运动的时间t2，很明显，t2＜t1．对于AEB段，由于其路程大，通过图象可知，可能时间比AB段短，可能比AB段长，但一定比ACD段长．故A正确，B、C、D错误．
故选A．
| 1 |
| 2 |
故选A．
练习册系列答案
初中学业考试导与练系列答案
相关题目
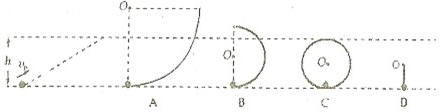
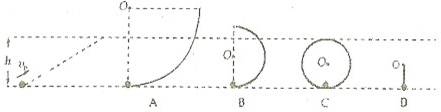
圆周轨道、B是半径小于h的光滑
圆周轨道、C是内轨直径等于h的光滑圆周轨道，小球均沿其轨道内侧运动．D是长为
h的轻棒、可绕O点做无摩擦转动，小球固定于其下端．小球在底端时的初速度都为v，则小球在以上四种情况中能到达高度h的有（ ）