题目内容
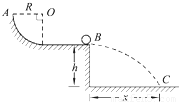
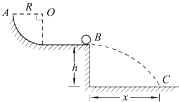 半径R=1m的四分之一圆弧轨道下端与一水平轨道连接,水平轨道离地面高度h=0.8m,如图所示,有一质量m=1.0kg的小滑块自圆轨道最高点A由静止开始滑下,经过水平轨道末端B,滑块最终落在地面上C点.经测量得x=1.6m(g取10m/s2)试求:
半径R=1m的四分之一圆弧轨道下端与一水平轨道连接,水平轨道离地面高度h=0.8m,如图所示,有一质量m=1.0kg的小滑块自圆轨道最高点A由静止开始滑下,经过水平轨道末端B,滑块最终落在地面上C点.经测量得x=1.6m(g取10m/s2)试求:(1)不计空气阻力,滑块落在地面上时速度vc多大?方向如何?
(2)滑块在AB轨道上滑行时克服摩擦力做功多少?
分析:(1)根据运动学公式,结合运动的合成与分解,即可求解;
(2)根据动能定理,即可求解.
(2)根据动能定理,即可求解.
解答:解:(1)小球B→C
x=vBt
h=
gt2
得vB=4 m/s
t=0.4 s
vy=gt=10×0.4=4 m/s
vc=
=4
m/s
由于水平方向速度与竖直方向速度相等,因此方向与水平夹角45°
(2)根据动能定理,则有mgR-Wf=
m
Wf=1×10×1-12×1×42=2 J
答:(1)不计空气阻力,滑块落在地面上时速度4
m/s;方向与水平夹角45°;
(2)滑块在AB轨道上滑行时克服摩擦力做功2 J.
x=vBt
h=
| 1 |
| 2 |
得vB=4 m/s
t=0.4 s
vy=gt=10×0.4=4 m/s
vc=
|
| 2 |
由于水平方向速度与竖直方向速度相等,因此方向与水平夹角45°
(2)根据动能定理,则有mgR-Wf=
| 1 |
| 2 |
| v | 2 B |
Wf=1×10×1-12×1×42=2 J
答:(1)不计空气阻力,滑块落在地面上时速度4
| 2 |
(2)滑块在AB轨道上滑行时克服摩擦力做功2 J.
点评:考查运动学公式与动能定理的应用,掌握运动的合成与分解,注意力做功的正负值.

练习册系列答案
相关题目
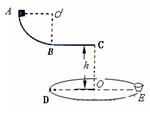
 (2013?德州一模)如图所示,一半径R=1m的圆盘水平放置,在其边缘 E点固定一小桶(可视为质点).在圆盘直径 DE 的正上方平行放置一水平滑道 BC,滑道右端 C点 与圆盘圆心O在同一竖直线上,且竖直高度 h=1.25m.AB为一竖直面内的光滑四分之一圆弧轨道,半径r=0.45m,且与水平滑道相切与B点.一质量m=0.2kg的滑块(可视为质点)从A点由静止释放,当滑块经过B点时,圆盘从图示位置以一定的角速度ω绕通过圆心的竖直轴匀速转动,最终物块由C 点水平抛出,恰好落入圆盘边缘的小桶内.已知滑块与滑道 BC间的摩擦因数μ=0.2.(取g=10m/s2)求
(2013?德州一模)如图所示,一半径R=1m的圆盘水平放置,在其边缘 E点固定一小桶(可视为质点).在圆盘直径 DE 的正上方平行放置一水平滑道 BC,滑道右端 C点 与圆盘圆心O在同一竖直线上,且竖直高度 h=1.25m.AB为一竖直面内的光滑四分之一圆弧轨道,半径r=0.45m,且与水平滑道相切与B点.一质量m=0.2kg的滑块(可视为质点)从A点由静止释放,当滑块经过B点时,圆盘从图示位置以一定的角速度ω绕通过圆心的竖直轴匀速转动,最终物块由C 点水平抛出,恰好落入圆盘边缘的小桶内.已知滑块与滑道 BC间的摩擦因数μ=0.2.(取g=10m/s2)求
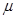 =0.2。(取g=10m/
=0.2。(取g=10m/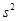 )
)