题目内容
 如图所示,将斜面体固定在水平面上,其两个斜面光滑,斜面上放置一质量不计的柔软薄纸带.现将质量为mA的A物体和质量为mB的B物体轻放在纸带上.两物体可视为质点,物体初始位置及数据如图所示.
如图所示,将斜面体固定在水平面上,其两个斜面光滑,斜面上放置一质量不计的柔软薄纸带.现将质量为mA的A物体和质量为mB的B物体轻放在纸带上.两物体可视为质点,物体初始位置及数据如图所示.
(1)若纸带与物体A、B间的动摩擦因数足够大,在纸带上同时放上A、B后,发现两物体恰好都能保持静止,则mA和mB应满足什么关系?
(2)若mA=2kg,mB=lkg,A与纸带间的动摩擦因数μA=0.5,B与纸带间的动摩擦因数μB=0.8,假设两物体与纸面间的滑动摩擦力与最大静摩擦力相等,试通过计算简要描述两物体同时从静止释放后的运动情况,并求出B物体自释放起经过多少时间到达斜面底端. (sin37°=0.6,cos37°=0.8,g取l0In/s2)
解:(1)由于纸带对A、B两个物体的摩擦力大小相等,系统处于平衡态,则
mAgsin53°=mBgsin37°
解得:mA:mB=3:4
(2)先假设纸带固定不动,再把物体A、B按题中条件放置在斜面上
对A物体受力分析计算得:mAgsin53°>μAmAgcos53°,则A相对纸带滑动;
对B物体受力分析计算得:mBgsin37°<μBmBgcos37°,则B相对纸带不滑动;
对B和纸带整体分析,A对纸带滑动摩擦力f=μAmAgcos53°=6N
B物体沿斜面分力mBgsin37°=6N
则说明若A、B和纸带同时释放后,B和纸带先静止不动,A沿纸带加速下滑1.6m后,B再拖动纸带一起沿光滑斜面加速下滑.
A沿纸带下滑过程中:
mAgsin53°-μAmAgcos53°=mAa1
解得:a1=gsin53°-μAgcos53°=5m/s2
根据位移时间公式,有x1=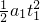 ,解得t1=0.8s
,解得t1=0.8s
B拖动纸带一起沿光滑斜面加速下滑过程中:
mBgsin37°=mBa2
解得:a2=gsin37°=6m/s2
根据位移时间公式,有x2= ,解得t2=1.0s
,解得t2=1.0s
则所求总时间t=t1+t2=1.8s
答:(1)mA和mB应满足关系为mA:mB=3:4;
(2)B物体自释放起经过1.8s时间到达斜面底端.
分析:(1)物体A、B均受力平衡,根据平衡条件列式求解即可;
(2)先假设纸带不动,判断出物体A和B的运动情况;然后得到物体A和B的实际运动情况,然后结合牛顿第二定律和运动学公式列式求解.
点评:本题关键是灵活选择研究对象,受力分析后确定物体的运动规律,最后结合运动学公式列式求解出物体的运动学参量.
mAgsin53°=mBgsin37°
解得:mA:mB=3:4
(2)先假设纸带固定不动,再把物体A、B按题中条件放置在斜面上
对A物体受力分析计算得:mAgsin53°>μAmAgcos53°,则A相对纸带滑动;
对B物体受力分析计算得:mBgsin37°<μBmBgcos37°,则B相对纸带不滑动;
对B和纸带整体分析,A对纸带滑动摩擦力f=μAmAgcos53°=6N
B物体沿斜面分力mBgsin37°=6N
则说明若A、B和纸带同时释放后,B和纸带先静止不动,A沿纸带加速下滑1.6m后,B再拖动纸带一起沿光滑斜面加速下滑.
A沿纸带下滑过程中:
mAgsin53°-μAmAgcos53°=mAa1
解得:a1=gsin53°-μAgcos53°=5m/s2
根据位移时间公式,有x1=
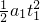 ,解得t1=0.8s
,解得t1=0.8sB拖动纸带一起沿光滑斜面加速下滑过程中:
mBgsin37°=mBa2
解得:a2=gsin37°=6m/s2
根据位移时间公式,有x2=
 ,解得t2=1.0s
,解得t2=1.0s则所求总时间t=t1+t2=1.8s
答:(1)mA和mB应满足关系为mA:mB=3:4;
(2)B物体自释放起经过1.8s时间到达斜面底端.
分析:(1)物体A、B均受力平衡,根据平衡条件列式求解即可;
(2)先假设纸带不动,判断出物体A和B的运动情况;然后得到物体A和B的实际运动情况,然后结合牛顿第二定律和运动学公式列式求解.
点评:本题关键是灵活选择研究对象,受力分析后确定物体的运动规律,最后结合运动学公式列式求解出物体的运动学参量.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目



 两点的相对距离不变,相对运动轨迹为圆弧,VA=VB+VAB,在AB连线上
两点的相对距离不变,相对运动轨迹为圆弧,VA=VB+VAB,在AB连线上

