题目内容
10. 如图,质量为m的小球,在半径为R的质量为M光滑圆形管道内做圆周运动,圆形管道竖直地放置在地面上,不会倾倒.小球的半径略微比管道的内径小一点,且远小于R可视为质点.求:
如图,质量为m的小球,在半径为R的质量为M光滑圆形管道内做圆周运动,圆形管道竖直地放置在地面上,不会倾倒.小球的半径略微比管道的内径小一点,且远小于R可视为质点.求:(1)若小球恰好能够通过最高点,那当小球运动到最低点时对圆管的作用力;
(2)若小球以某一速度运动到最高点时,地面对圆管恰好无支持力,求小球运动到最低点时地面对圆管的作用力.
分析 (1)圆形管道内能支撑小球,小球能够通过最高点时的最小速度为0,根据动能定理求出最低点的速度,再根据向心力公式求解;
(2)地面对圆管恰好无支持力,则小球对圆管向上的压力等于圆管的重力,根据牛顿第三定律可知,圆管对小球的压力T2=Mg,小球在最高点,根据向心力公式求出速度,从最高点到最低点的过程中,根据动能定理求出最低点速度,在最低点,根据向心力公式求出圆管对小球的作用力,根据牛顿第三定律可知,小球对圆管向下的压力,对圆管受力分析,根据平衡条件求出地面的支持力.
解答 解:(1)小球恰好能够通过最高点,则到达最高点的速度为零,从最高点到最低点的过程中,根据动能定理得:
$\frac{1}{2}m{{v}_{1}}^{2}=mg•2R$
在最低点,根据向心力公式得:
T1-mg=m$\frac{{{v}_{1}}^{2}}{R}$
解得:T1=5mg,
根据牛顿第三定律可知,小球对圆管的作用力大小为5mg,方向向上,
(2)若小球以某一速度运动到最高点时,地面对圆管恰好无支持力,则小球对圆管向上的压力等于圆管的重力,根据牛顿第三定律可知,圆管对小球的压力为:
T2=Mg…①,
小球在最高点,根据向心力公式得:
${T}_{2}+mg=m\frac{{{v}_{2}}^{2}}{R}$…②
从最高点到最低点的过程中,根据动能定理得:
$\frac{1}{2}m{{v}_{3}}^{2}-\frac{1}{2}m{{v}_{2}}^{2}=mg•2R$…③,
在最低点,根据向心力公式得:
${T}_{3}-mg=m\frac{{{v}_{3}}^{2}}{R}$…④
由①②③④解得:
T3=6mg+Mg
根据牛顿第三定律可知,小球对圆管向下的压力为:T4=T3=6mg+Mg,
圆管处于静止状态,则地面对圆管的支持力为:FN=T4+Mg=6mg+2Mg,方向向上.
答:(1)若小球恰好能够通过最高点,那当小球运动到最低点时对圆管的作用力大小为5mg,方向向上;
(2)小球运动到最低点时地面对圆管的作用力大小为6mg+2Mg,方向向上.
点评 本题主要考查了动能定理、向心力公式以及牛顿第二定律的直接应用,解题时关键抓住小球恰好能够通过最高点,则到达最高点的速度为零以及地面对圆管恰好无支持力,则小球对圆管向上的压力等于圆管的重力求解,难度适中.

| A. | 向心力不改变做匀速圆周运动物体速度的大小 | |
| B. | 做匀速圆周运动的物体,其向心力是不变的 | |
| C. | 做圆周运动的物体,所受合力一定等于向心力 | |
| D. | 做匀速圆周运动的物体,一定是所受的合外力充当向心力 |
 如图,在地面上以速度υ0抛出质量为m的物体,抛出后物体落在比地面低h的海平面上,若以地面为零势能参考面,且不计空气阻力,则( )
如图,在地面上以速度υ0抛出质量为m的物体,抛出后物体落在比地面低h的海平面上,若以地面为零势能参考面,且不计空气阻力,则( )| A. | 物体在海平面的重力势能为mgh | |
| B. | 重力对物体做的功为-mgh | |
| C. | 物体在海平面上的动能为$\frac{1}{2}$mv02+mgh | |
| D. | 物体在海平面上的机械能为$\frac{1}{2}$mv02+mgh |
| A. | 小鸟的运动路程为80m | B. | 小鸟的平均速度为3m/s | ||
| C. | 甲、乙两车的位移之比为3:7 | D. | 小鸟的平均速度为7m/s |
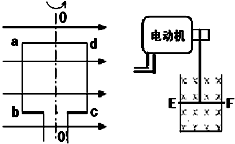 如图所示,一个矩形线圈的ab、cd边长为L1,ad、bc边长为L2,线圈的匝数为N,线圈处于磁感应强度为B的匀强磁场中,并以OO′为中轴做匀速圆周运动,(OO′与磁场方向垂直,线圈电阻不计),线圈转动的角速度为ω,设转动从中性面开始计时,请回答下列问题:
如图所示,一个矩形线圈的ab、cd边长为L1,ad、bc边长为L2,线圈的匝数为N,线圈处于磁感应强度为B的匀强磁场中,并以OO′为中轴做匀速圆周运动,(OO′与磁场方向垂直,线圈电阻不计),线圈转动的角速度为ω,设转动从中性面开始计时,请回答下列问题:
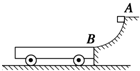 一个平板小车置于光滑水平面上,其右端恰好和一个$\frac{1}{4}$光滑圆弧轨道AB的底端等高对接,如图所示.已知小车质量M=3.0kg,长L=2.06m,圆弧轨道半径R=0.8m,现将一质量m=1.0kg的小滑块由轨道顶端A点无初速释放,滑块滑到B端后冲上小车.滑块与小车上表面间的动摩擦因数μ=0.3.(取g=10m/s2),试求:
一个平板小车置于光滑水平面上,其右端恰好和一个$\frac{1}{4}$光滑圆弧轨道AB的底端等高对接,如图所示.已知小车质量M=3.0kg,长L=2.06m,圆弧轨道半径R=0.8m,现将一质量m=1.0kg的小滑块由轨道顶端A点无初速释放,滑块滑到B端后冲上小车.滑块与小车上表面间的动摩擦因数μ=0.3.(取g=10m/s2),试求: 如图所示,质量为m=2kg的小球从R=40cm的$\frac{1}{4}$竖直圆弧轨道的顶端A点右静止开始下滑,通过圆弧轨道最低点B后做平抛运动,已知B点到地面的竖直高度H=45cm,B点与落地点C点的水平距离L=60cm,不计空气阻力,g取10m/s2,则:
如图所示,质量为m=2kg的小球从R=40cm的$\frac{1}{4}$竖直圆弧轨道的顶端A点右静止开始下滑,通过圆弧轨道最低点B后做平抛运动,已知B点到地面的竖直高度H=45cm,B点与落地点C点的水平距离L=60cm,不计空气阻力,g取10m/s2,则: