题目内容
17.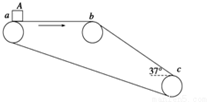 如图所示,传送带的水平部分ab=4m,斜面部分bc=4m,bc与水平面的夹角α=37°.一个小物体A与传送带的动摩擦因数μ=0.25,传送带沿图示的方向运动,速率v=2m/s.若把物体A轻放到a处,它将被传送带送到c点,且物体A不会脱离传送带.求物体A从a点被传送到c点所用的时间.(已知:sin 37°=0.6,cos 37°=0.8,g=10m/s2)
如图所示,传送带的水平部分ab=4m,斜面部分bc=4m,bc与水平面的夹角α=37°.一个小物体A与传送带的动摩擦因数μ=0.25,传送带沿图示的方向运动,速率v=2m/s.若把物体A轻放到a处,它将被传送带送到c点,且物体A不会脱离传送带.求物体A从a点被传送到c点所用的时间.(已知:sin 37°=0.6,cos 37°=0.8,g=10m/s2)
分析 物体在水平传送带上先做匀加速直线运动,达到传送带速度后做匀速直线运动,在倾斜传送带上,由于重力沿斜面方向的分力大于滑动摩擦力,所以物体做匀加速直线运动,根据牛顿第二定律求出在水平传送带和倾斜传送带上的加速度,结合运动学公式进行求解.
解答 解:物体A轻放在a点后在摩擦力作用下向右做匀加速直线运动直到和传送带速度相等.在这一过程中有a1=$\frac{μmg}{m}$=μg
x1=$\frac{{v}^{2}}{2a}=\frac{{v}^{2}}{2μg}$=0.8 m<ab.
经历时间为t1=$\frac{v}{{a}_{1}}$=$\frac{2}{2.5}$=0.8 s.
此后随传送带运动到b点的时间为t2=$\frac{ab-{x}_{1}}{v}$=$\frac{4-0.8}{2}$=1.6s.
当物体A到达bc斜面时,由于mgsin 37°=0.6mg>μmgcos 37°=0.2mg.所以物体A将再次沿传送带做匀加速直线运动,
其加速度大小为a2=gsin 37°-μgcos 37°=4 m/s2,
物体A在传送带bc上所用时间满足xbc=vt3+$\frac{1}{2}$a2t${\;}_{3}^{2}$,代入数据得t3=1 s.(负值舍去)
则物体A从a点被传送到c所用时间为t=t1+t2+t3=0.8+1.6+1=3.4 s.
答:物体A从a点被传送到c点所用的时间为3.4s.
点评 解决本题的关键理清物体在传送带上整个过程中的运动规律,结合牛顿第二定律和运动学公式进行求解,难度中等.

练习册系列答案
相关题目
7.永川兴龙湖中安装了音乐喷泉,夜晚开放时随音乐变换.当音乐高潮时,组合喷泉全部喷嘴竖直向上,喷出的水量Q=3000L/min,水的流速v0=15m/s,不计空气阻力,则稳定后空中的水的体积V应是(取g=10m/s2)( )
| A. | 75L | B. | 100L | C. | 150L | D. | 300L |
5.下列关于重力、弹力和摩擦力的说法,正确的是( )
| A. | 物体的重心并不一定在物体的几何中心上 | |
| B. | 劲度系数越大的弹簧,产生的弹力越大 | |
| C. | 动摩擦因数与物体之间的压力成反比,与滑动摩擦力成正比 | |
| D. | 静摩擦力的大小与物体之间的正压力成正比 |
12.下列说法正确的是( )
| A. | 光导纤维传输信号是利用光的干涉现象 | |
| B. | 全息照相利用了激光相干性好的特性 | |
| C. | 光的偏振现象说明光是横波 | |
| D. | X射线比无线电波更容易发生干涉和衍射现象 | |
| E. | 刮胡须的刀片的影子边缘模糊不清是光的衍射现象 |
2.下列说法正确的是( )
| A. | 第一宇宙速度7.9km/s是人造卫星绕地球飞行的最小速度 | |
| B. | 发射速度大于7.9km/s而小于第二宇宙速度时人造卫星将沿椭圆轨道运动 | |
| C. | 如果通信需要,地球的同步卫星可以定点在北京的上空 | |
| D. | 地球同步卫星的轨道可以是圆的,也可以是椭圆的 |
9.北京获得2022年冬奥会举办权,冰壶是冬奥会的比赛项目.将一个冰壶以一定初速度推出后将运动一段距离停下来.换一个材料相同,质量更大的冰壶,以相同的初速度推出后,冰壶运动的距离将( )
| A. | 不变 | B. | 变小 | C. | 变大 | D. | 无法判断 |
8.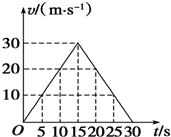 下表是通过测量得到的一辆摩托车沿直线做加速运动时的速度随时间的变化.
下表是通过测量得到的一辆摩托车沿直线做加速运动时的速度随时间的变化.
请根据测量数据和速度图象:
(1)求摩托车在第一个10s内的加速度.
(2)求摩托车在最后15s内的加速度.
(3)求摩托车在总过程中的位移.
 下表是通过测量得到的一辆摩托车沿直线做加速运动时的速度随时间的变化.
下表是通过测量得到的一辆摩托车沿直线做加速运动时的速度随时间的变化.| t/s | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| v/ (m•s-1) | 0 | 10 | 20 | 30 | 20 | 10 | 0 |
(1)求摩托车在第一个10s内的加速度.
(2)求摩托车在最后15s内的加速度.
(3)求摩托车在总过程中的位移.
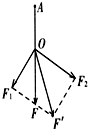 在探究合力的方法时,先将橡皮条的一端固定在水平木板上,另一端系上带有绳套的两根细绳.实验时,需要两次拉伸橡皮条,一次是通过两细绳用两个弹簧秤互成角度地拉橡皮条,另一次是用一个弹簧秤通过细绳拉橡皮条.
在探究合力的方法时,先将橡皮条的一端固定在水平木板上,另一端系上带有绳套的两根细绳.实验时,需要两次拉伸橡皮条,一次是通过两细绳用两个弹簧秤互成角度地拉橡皮条,另一次是用一个弹簧秤通过细绳拉橡皮条. 如图的一簇平行线为未知方向的匀强电场的电场线.沿与平行线成60°角的方向,把1×10-6C的正电荷从A点移到B点,电场力做了2×10-6J的功,AB间距离为2cm,问:
如图的一簇平行线为未知方向的匀强电场的电场线.沿与平行线成60°角的方向,把1×10-6C的正电荷从A点移到B点,电场力做了2×10-6J的功,AB间距离为2cm,问: