题目内容
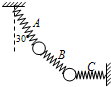 如图所示,用完全相同的轻弹簧A、B、C将两个相同的小球连接并悬挂,小球处于静止状态,弹簧A与竖直方向的夹角为30°,弹簧C水平,则弹簧A、C的伸长量之比为( )
如图所示,用完全相同的轻弹簧A、B、C将两个相同的小球连接并悬挂,小球处于静止状态,弹簧A与竖直方向的夹角为30°,弹簧C水平,则弹簧A、C的伸长量之比为( )分析:将两球和弹簧B看成一个整体,分析受力情况,根据平衡条件求出弹簧A、C拉力之比,即可由胡克定律得到伸长量之比.
解答:解:将两球和弹簧B看成一个整体,整体受到总重力G、弹簧A和C的拉力,如图,设弹簧A、C的拉力分别为F1和F2.由平衡条件得知,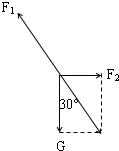 F2和G的合力与F1大小相等、方向相反
F2和G的合力与F1大小相等、方向相反
则得:F2=F1sin30°=0.5F1.
根据胡克定律得:F=kx,k相同,则 弹簧A、C的伸长量之比等于两弹簧拉力之比,即有xA:xC=F1:F2=2:1
故选D
 F2和G的合力与F1大小相等、方向相反
F2和G的合力与F1大小相等、方向相反则得:F2=F1sin30°=0.5F1.
根据胡克定律得:F=kx,k相同,则 弹簧A、C的伸长量之比等于两弹簧拉力之比,即有xA:xC=F1:F2=2:1
故选D
点评:本题首先要选择好研究对象,其次正确分析受力情况,作出力图,再由平衡条件求解.

练习册系列答案
相关题目
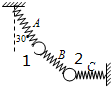 如图所示,用完全相同的轻弹簧A、B、C将两个小球1、2连接并悬挂,小球均处于静止状态,小球1、2的质量分别为2m和m.弹簧A与竖直方向的夹角为30°,弹簧C水平,则弹簧A、B、C的伸长量之比为( )
如图所示,用完全相同的轻弹簧A、B、C将两个小球1、2连接并悬挂,小球均处于静止状态,小球1、2的质量分别为2m和m.弹簧A与竖直方向的夹角为30°,弹簧C水平,则弹簧A、B、C的伸长量之比为( )A、
| ||||
B、4:
| ||||
C、2
| ||||
D、2
|


 ∶4 B..4∶
∶4 B..4∶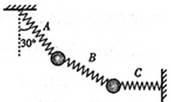
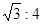 B.
B.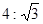 C.1:2 D. 2:1
C.1:2 D. 2:1