题目内容
5.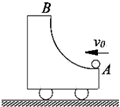 如图所示,在光滑水平面上停放着质量为m且装有光滑的弧形槽轨道AB的小车,轨道A端的切线水平.一质量为m的小球以水平的速度vo从小车右边沿弧形槽轨道A端滑上小车,到达某一高度后,小球又返回弧形槽轨道A端,则下列判断正确的是( )
如图所示,在光滑水平面上停放着质量为m且装有光滑的弧形槽轨道AB的小车,轨道A端的切线水平.一质量为m的小球以水平的速度vo从小车右边沿弧形槽轨道A端滑上小车,到达某一高度后,小球又返回弧形槽轨道A端,则下列判断正确的是( )| A. | 小球离开小车后,向右做平抛运动 | |
| B. | 小球离开小车后,向左做平抛运动 | |
| C. | 此过程中小球对车做功为$\frac{1}{2}$mv02 | |
| D. | 小球沿小车的弧形槽轨道上升的最大度为$\frac{v_0^2}{2g}$ |
分析 小球和小车组成的系统在水平方向上动量守恒,当小球上升的最高点时,竖直方向上的速度为零,水平方向上与小车具有相同的速度,结合动量守恒和能量守恒求出上升的最大高度.根据动量守恒定律和能量守恒求出小球返回右端时的速度,从而得出小球的运动规律,根据动能定理得出小球对小车做功的大小.
解答 解:A、设小球离开小车时,小球的速度为v1,小车的速度为v2,整个过程中动量守恒,得:mv0=mv1+mv2…①,
由动能守恒得:$\frac{1}{2}$mv02=$\frac{1}{2}$mv12+$\frac{1}{2}$mv22…②,联立①②,解得:v1=0,v2=v0,
即小球与小车分离后二者交换速度,所以小球与小车分离后做自由落体运动,故AB错误.
C、对小车运用动能定理得,小球对小车做功:W=$\frac{1}{2}$mv02-0=$\frac{1}{2}$mv02,故C正确.
D、当小球与小车的水平速度相等时,小球弧形槽上升到最大高度,设该高度为h,则:mv0=2m•v…③,$\frac{1}{2}$mv02=$\frac{1}{2}$•2mv2+mgh …④,联立③④解得:h=$\frac{{v}_{0}^{2}}{4g}$,故D错误.
故选:C.
点评 本题考查了动量守恒定律和能量守恒定律的综合,知道当小球与小车的水平速度相等时,小球上升到最大高度.

练习册系列答案
相关题目
16.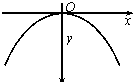 如图所示,两个物体以相同大小的初始速度从空中O点同时分别向x轴正负方向水平抛出,它们的轨迹恰好是抛物线方程y=$\frac{1}{k}$x2,重力加速度为g,那么以下说法正确的是(曲率半径可认为等于曲线上该点的瞬时速度所对应的匀速率圆周运动的半径)( )
如图所示,两个物体以相同大小的初始速度从空中O点同时分别向x轴正负方向水平抛出,它们的轨迹恰好是抛物线方程y=$\frac{1}{k}$x2,重力加速度为g,那么以下说法正确的是(曲率半径可认为等于曲线上该点的瞬时速度所对应的匀速率圆周运动的半径)( )
 如图所示,两个物体以相同大小的初始速度从空中O点同时分别向x轴正负方向水平抛出,它们的轨迹恰好是抛物线方程y=$\frac{1}{k}$x2,重力加速度为g,那么以下说法正确的是(曲率半径可认为等于曲线上该点的瞬时速度所对应的匀速率圆周运动的半径)( )
如图所示,两个物体以相同大小的初始速度从空中O点同时分别向x轴正负方向水平抛出,它们的轨迹恰好是抛物线方程y=$\frac{1}{k}$x2,重力加速度为g,那么以下说法正确的是(曲率半径可认为等于曲线上该点的瞬时速度所对应的匀速率圆周运动的半径)( )| A. | 初始速度为$\sqrt{2kg}$ | B. | 初始速度为$\sqrt{kg}$ | ||
| C. | O点的曲率半径为$\frac{k}{2}$ | D. | O点的曲率半径为2k |
13.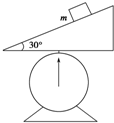 如图所示,在托盘测力计的托盘内固定一个倾角为30°的斜面,现将一个重为4N的物体放在斜面上,让它自由下滑,那么测力计因4N物体的存在而增加的读数不可能是.( )
如图所示,在托盘测力计的托盘内固定一个倾角为30°的斜面,现将一个重为4N的物体放在斜面上,让它自由下滑,那么测力计因4N物体的存在而增加的读数不可能是.( )
 如图所示,在托盘测力计的托盘内固定一个倾角为30°的斜面,现将一个重为4N的物体放在斜面上,让它自由下滑,那么测力计因4N物体的存在而增加的读数不可能是.( )
如图所示,在托盘测力计的托盘内固定一个倾角为30°的斜面,现将一个重为4N的物体放在斜面上,让它自由下滑,那么测力计因4N物体的存在而增加的读数不可能是.( )| A. | 2N | B. | 3N | C. | 2$\sqrt{3}$N | D. | 4N |
10.质量为m的物体,在水平力F作用下,在粗糙的水平面上运动,下列哪些说法正确( )
| A. | 如果物体做加速直线运动,F一定对物体做正功 | |
| B. | 如果物体做减速直线运动,F一定对物体做负功 | |
| C. | 如果物体做减速直线运动,F也可能对物体做正功 | |
| D. | 如果物体做匀速直线运动,F一定对物体做正功 |
17.如图,一铝块正由左向右滑动穿过线圈,那么下面不正确的判断是( )


| A. | 接近线圈时做加速运动,离开时做减速运动 | |
| B. | 接近和离开线圈时都做减速运动 | |
| C. | 一直在做匀速运动 | |
| D. | 在线圈中运动时是匀速的 |
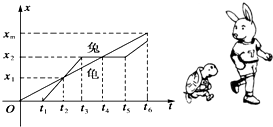 小李讲了一个龟兔赛跑的故事,按照小李讲的故事情节,作出兔子和乌龟的位移图象如图所示,请你依照图象中的坐标,并结合物理学的术语来讲述这个故事.你在讲故事之前,先回答下列问题.
小李讲了一个龟兔赛跑的故事,按照小李讲的故事情节,作出兔子和乌龟的位移图象如图所示,请你依照图象中的坐标,并结合物理学的术语来讲述这个故事.你在讲故事之前,先回答下列问题.