题目内容
19.做匀速圆周运动的物体,10s内沿半径是20m的圆周运动了100m,则求(1)线速度大小
(2)周期
(3)角速度.
分析 (1)根据$v=\frac{△s}{△t}$求出匀速圆周运动的线速度大小.
(2)根据T=$\frac{2πr}{v}$求出运动的周期.
(3)根据ω=$\frac{2π}{T}$求出角速度的大小.
解答 解:(1)由线速度定义得:线速度的大小为:$v=\frac{△s}{△t}=\frac{100}{10}m/s=10m/s$
(2)周期为:$T=\frac{2πr}{v}=\frac{2π×20}{10}s=4πs=12.56s$
(3)角速度ω=$\frac{2π}{T}=\frac{2π}{4π}rad/s=0.5rad/s$.
答:(1)线速度大小为10m/s;
(2)周期为12.56s;
(3)角速度为0.5rad/s.
点评 解决本题的关键掌握线速度的定义,然后根据线速度、角速度、周期的关系求解.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
18.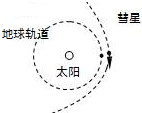 据报道,2011年10月16日,被末日论和阴谋论者认定为“末日彗星”的埃里宁彗星掠过近日点,正巧也是最接近地球的位置,正巧也是最接近地球的位置,不过它和地球之间的最近距离仍有大约3540万公里,相比月球到地球的距离38万公里还是要大很多,如图所示.已知地球绕太阳在半径为1.5×1011m的圆轨道上运动,周期为1年;该彗星因受太阳的引力,沿椭圆轨道绕太阳运动,其椭圆轨道的长轴是地球公转轨道半径的529倍(即232倍).引力常量已知为G=6.67×10-11 N•m2/kg2.则由上述信息( )
据报道,2011年10月16日,被末日论和阴谋论者认定为“末日彗星”的埃里宁彗星掠过近日点,正巧也是最接近地球的位置,正巧也是最接近地球的位置,不过它和地球之间的最近距离仍有大约3540万公里,相比月球到地球的距离38万公里还是要大很多,如图所示.已知地球绕太阳在半径为1.5×1011m的圆轨道上运动,周期为1年;该彗星因受太阳的引力,沿椭圆轨道绕太阳运动,其椭圆轨道的长轴是地球公转轨道半径的529倍(即232倍).引力常量已知为G=6.67×10-11 N•m2/kg2.则由上述信息( )
 据报道,2011年10月16日,被末日论和阴谋论者认定为“末日彗星”的埃里宁彗星掠过近日点,正巧也是最接近地球的位置,正巧也是最接近地球的位置,不过它和地球之间的最近距离仍有大约3540万公里,相比月球到地球的距离38万公里还是要大很多,如图所示.已知地球绕太阳在半径为1.5×1011m的圆轨道上运动,周期为1年;该彗星因受太阳的引力,沿椭圆轨道绕太阳运动,其椭圆轨道的长轴是地球公转轨道半径的529倍(即232倍).引力常量已知为G=6.67×10-11 N•m2/kg2.则由上述信息( )
据报道,2011年10月16日,被末日论和阴谋论者认定为“末日彗星”的埃里宁彗星掠过近日点,正巧也是最接近地球的位置,正巧也是最接近地球的位置,不过它和地球之间的最近距离仍有大约3540万公里,相比月球到地球的距离38万公里还是要大很多,如图所示.已知地球绕太阳在半径为1.5×1011m的圆轨道上运动,周期为1年;该彗星因受太阳的引力,沿椭圆轨道绕太阳运动,其椭圆轨道的长轴是地球公转轨道半径的529倍(即232倍).引力常量已知为G=6.67×10-11 N•m2/kg2.则由上述信息( )| A. | 可求出该彗星绕太阳运动的周期是12167年 | |
| B. | 可求出该彗星的质量 | |
| C. | 可求出太阳对该彗星的引力 | |
| D. | 可求出太阳的质量 |
10.下列说法正确的是( )
| A. | 汤姆孙发现电子,提出原子的核式结构模型 | |
| B. | 金属的逸出功随入射光的频率增大而增大 | |
| C. | 核力存在于原子核内所有核子之间 | |
| D. | 核电站是利用重核裂变反应所释放的核能转化为电能 |
4.下列关于万有引力定律的说法中,正确的是( )
| A. | 万有引力定律是卡文迪许在实验室中发现的 | |
| B. | 对于相距很远、可以看成质点的两个物体,万有引力定律F=G$\frac{Mm}{r^2}$中的r是两质点间的距离 | |
| C. | 对于质量分布均匀的球体,公式中的r是两球心间的距离 | |
| D. | 质量大的物体对质量小的物体的引力大于质量小的物体对质量大的物体的引力 |
11.下列数据最接近实际情况的是( )
| A. | 使人感到舒适的温度约是23℃ | |
| B. | 台灯正常工作时的电流约是2A | |
| C. | 中学生步行的速度约是5m/s | |
| D. | 中学生从一楼匀速上到三楼所做的功约是300J |
8. 在测量某弹簧的劲度系数时,某同学讲该弹簧沿竖直方向悬挂起来,在另一端挂上不同质量的钩码,测出钩码质量和弹簧长度L的相应数据如表所示:
在测量某弹簧的劲度系数时,某同学讲该弹簧沿竖直方向悬挂起来,在另一端挂上不同质量的钩码,测出钩码质量和弹簧长度L的相应数据如表所示:
(1)在如图所示的坐标系中作出m-L关系图象.
(2)根据所作的图线可得弹簧的劲度系数为10N/m(g取10m/s2).
 在测量某弹簧的劲度系数时,某同学讲该弹簧沿竖直方向悬挂起来,在另一端挂上不同质量的钩码,测出钩码质量和弹簧长度L的相应数据如表所示:
在测量某弹簧的劲度系数时,某同学讲该弹簧沿竖直方向悬挂起来,在另一端挂上不同质量的钩码,测出钩码质量和弹簧长度L的相应数据如表所示:| 钩码质量(g) | 0 | 20 | 40 | 60 | 80 | 100 |
| 弹簧长度(cm) | 15.0 | 17.1 | 19.0 | 20.9 | 23.0 | 25.1 |
(2)根据所作的图线可得弹簧的劲度系数为10N/m(g取10m/s2).
9.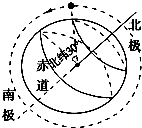 极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道).如图所示,若某极地卫星从北纬30°的正上方按图示方向第一次运行至南纬60°正上方,所用时间为t,已知地球半径为R(地球可看做球体),地球表面的重力加速度为g,引力常量为G,由以上条件可知( )
极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道).如图所示,若某极地卫星从北纬30°的正上方按图示方向第一次运行至南纬60°正上方,所用时间为t,已知地球半径为R(地球可看做球体),地球表面的重力加速度为g,引力常量为G,由以上条件可知( )
 极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道).如图所示,若某极地卫星从北纬30°的正上方按图示方向第一次运行至南纬60°正上方,所用时间为t,已知地球半径为R(地球可看做球体),地球表面的重力加速度为g,引力常量为G,由以上条件可知( )
极地卫星的运行轨道平面通过地球的南北两极(轨道可视为圆轨道).如图所示,若某极地卫星从北纬30°的正上方按图示方向第一次运行至南纬60°正上方,所用时间为t,已知地球半径为R(地球可看做球体),地球表面的重力加速度为g,引力常量为G,由以上条件可知( )| A. | 地球的质量为$\frac{gR}{G}$ | |
| B. | 卫星运行的线速度为$\frac{πR}{2t}$ | |
| C. | 卫星运行的角速度为$\frac{π}{2t}$ | |
| D. | 卫星距地面的高度为($\frac{4g{R}^{2}{t}^{2}}{{π}^{2}}$)${\;}^{\frac{1}{3}}$ |
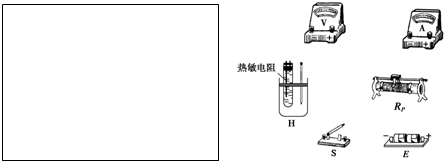
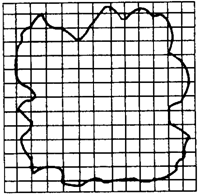 在课本上粗测油酸分子的大小的实验中,油酸酒精溶液的浓度为每104mL溶液中有纯油酸6mL,用注射器量得1mL上述溶液有75滴,把一滴该溶液滴入盛水的表面撒有痱子粉的浅盘里,待水面稳定后,测得油酸膜的近似轮廓如图所示,图中正方形小方格的边长为1cm.则
在课本上粗测油酸分子的大小的实验中,油酸酒精溶液的浓度为每104mL溶液中有纯油酸6mL,用注射器量得1mL上述溶液有75滴,把一滴该溶液滴入盛水的表面撒有痱子粉的浅盘里,待水面稳定后,测得油酸膜的近似轮廓如图所示,图中正方形小方格的边长为1cm.则