题目内容
4. 如图所示,在坐标系的第一、四象限存在一宽度为a、垂直纸面向外的有界匀强磁场,磁感应强度的大小为B;在第三象限存在与y轴正方向成θ=60°角的匀强电场.一个粒子源能释放质量为m、电荷量为+q的粒子,粒子的初速度可以忽略.粒子源在点P(-$\frac{\sqrt{3}}{2}$a,-$\frac{1}{2}$a)时发出的粒子恰好垂直磁场边界EF射出;将粒子源沿直线PO移动到Q点时,所发出的粒子恰好不能从EF射出.不计粒子的重力及粒子间相互作用力.求:
如图所示,在坐标系的第一、四象限存在一宽度为a、垂直纸面向外的有界匀强磁场,磁感应强度的大小为B;在第三象限存在与y轴正方向成θ=60°角的匀强电场.一个粒子源能释放质量为m、电荷量为+q的粒子,粒子的初速度可以忽略.粒子源在点P(-$\frac{\sqrt{3}}{2}$a,-$\frac{1}{2}$a)时发出的粒子恰好垂直磁场边界EF射出;将粒子源沿直线PO移动到Q点时,所发出的粒子恰好不能从EF射出.不计粒子的重力及粒子间相互作用力.求:(1)匀强电场的电场强度;
(2)PQ的长度;
(3)若仅将电场方向沿顺时针方向转动60°角,粒子源仍在PQ间移动并释放粒子,试判断这些粒子第一次从哪个边界射出磁场并确定射出点的纵坐标范围.
分析 (1)对直线加速过程根据动能定理列式,画出轨迹后结合几何关系确定轨道半径,然后根据牛顿第二定律列式求解;
(2)先对从Q到O过程根据动能定理列式求解,再次画出轨迹后结合几何关系确定轨道半径,最后根据牛顿第二定律列式求解;
(3)先根据动能定理确定进入磁场的初速度,然后画出轨道,结合几何关系确定射出点.
解答 解:(1)粒子源在P点时,粒子在电场中被加速;
点P坐标为:(-$\frac{\sqrt{3}}{2}$a,-$\frac{1}{2}$a),故PO=$\sqrt{(\frac{\sqrt{3}}{2}a)^{2}+(\frac{1}{2}a)^{2}}=a$
根据动能定理,有:
qEa=$\frac{1}{2}m{v}_{1}^{2}$
解得:
${v}_{1}=\sqrt{\frac{2qEa}{m}}$ 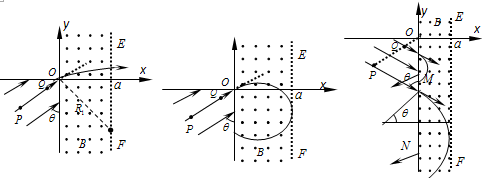
粒子在磁场中做匀速圆周运动,根据牛顿第二定律,有:
q${v}_{1}B=m\frac{{v}_{1}^{2}}{{R}_{1}}$
由几何关系知,半径:
${R}_{1}=\frac{a}{cosθ}$=2a
解得:
E=$\frac{2q{B}^{2}a}{m}$
(2)粒子源在Q点时,设OQ=d,根据动能定理,有:
qEd=$\frac{1}{2}m{v}_{2}^{2}$
根据牛顿第二定律,有:
q${v}_{2}B=m\frac{{v}_{2}^{2}}{{R}_{2}}$
粒子在磁场中运动轨迹与边界EF相切,由几何关系知:
R2cos60°+R2=a
R${\;}_{2}=\frac{2}{3}a$
联立解得:
d=$\frac{a}{9}$
长度:PQ=OP-OQ=$\frac{8a}{9}$
(3)若将电场方向变为与y轴负方向成θ=60°角,由于加速距离相等,电场力大小也相等,粒子源在P、Q两点处时,粒子经电场加速后到进入磁场时的速率与第一问中速率相等,仍为v1、v2.从P、Q点发出的粒子在磁场中的轨道半径仍为:R1=2a、R2=$\frac{2}{3}a$;
从P发出的粒子第一次从y轴上N点射出,由几何关系知轨道正好与EF相切,N点的纵坐标:${y}_{N}=-(a+2{R}_{1}sin60°)=-(1+2\sqrt{3})a$
同理可求,从Q发出的粒子第一次从y轴上M点射出,M点的纵坐标:
${y}_{N}=-(\frac{1}{9}a+2{R}_{2}sin60°)=-\frac{(1+6\sqrt{3})a}{9}$
即射出点的纵坐标范围[$-\frac{(1+6\sqrt{3})a}{9}$,$-(1+2\sqrt{3})a$]
答:(1)匀强电场的电场强度为$\frac{2q{B}^{2}a}{m}$;
(2)PQ的长度为$\frac{8a}{9}$;
(3)这些粒子第一次从左边界射出磁场,射出点的纵坐标范围为[$-\frac{(1+6\sqrt{3})a}{9}$,$-(1+2\sqrt{3})a$].
点评 本题关键是明确粒子的运动规律,画出运动轨迹,然后分阶段根据动能定理,牛顿第二定律列式求解.

| A. | $\frac{N}{μ}$,$\frac{ρN}{μ}$ | B. | $\frac{N}{μ}$,$\frac{Nμ}{ρ}$ | C. | $\frac{ρN}{μ}$,$\frac{N}{ρ}$ | D. | $\frac{N}{ρ}$,$\frac{ρN}{μ}$ |

| A. | 当r=r0时,分子为零,分子势能最小也为零 | |
| B. | 当r>r0时,分子力和分子势能都随距离的增大而增大 | |
| C. | 在两分子由无穷远逐渐靠近直至距离最小的过程中分子力先做正功后做负功 | |
| D. | 在两分子由无穷远逐渐靠近直至距离最小的过程中分子势能先增大,后减小,最后又增大 |
| A. | 平均速度的公式v=$\frac{x}{t}$ | B. | 电场中某点电势Φ=$\frac{{E}_{P}}{q}$ | ||
| C. | 磁感应强度B=$\frac{F}{IL}$ | D. | 电容 C=$\frac{Q}{U}$ |
 如图所示,一滑块从固定的斜面底端A处冲上粗糙的斜面,到达某一高度后返回A.下列各图分别表示滑块在斜面上运动的速度v、加速度a、势能Ep、机械能E随时间变化的图象,可能正确的是( )
如图所示,一滑块从固定的斜面底端A处冲上粗糙的斜面,到达某一高度后返回A.下列各图分别表示滑块在斜面上运动的速度v、加速度a、势能Ep、机械能E随时间变化的图象,可能正确的是( )| A. |  | B. |  | C. | 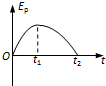 | D. | 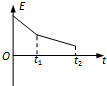 |
 民族运动会上有一骑射项目如图所示,运动员骑在奔跑的马上,弯弓放箭射击侧向的固定目标.假设运动员骑马奔驰的速度为v1,运动员静止时射出的弓箭速度为v2,跑道离固定目标的最近距离为d,要想命中目标且射出的箭在空中飞行时间最短,则( )
民族运动会上有一骑射项目如图所示,运动员骑在奔跑的马上,弯弓放箭射击侧向的固定目标.假设运动员骑马奔驰的速度为v1,运动员静止时射出的弓箭速度为v2,跑道离固定目标的最近距离为d,要想命中目标且射出的箭在空中飞行时间最短,则( )| A. | 运动员放箭处离目标的距离为$\frac{d{v}_{2}}{{v}_{1}}$ | |
| B. | 运动员放箭处离目标的距离为$\frac{d\sqrt{{{v}_{1}}^{2}+{{v}_{2}}^{2}}}{2{v}_{2}}$ | |
| C. | 箭射到固定目标的最短时间为$\frac{d}{{v}_{2}}$ | |
| D. | 箭射到固定目标的最短时间为$\frac{d}{\sqrt{{{v}_{2}}^{2}-{{v}_{1}}^{2}}}$ |
| A. | 400 W | B. | 300W | C. | 200 W | D. | 100 W |
 如图所示,电路中的变压器为理想变压器,S为单刀双掷开关.P是滑动变阻器R的滑动触头,U1为加在原线圈两端的交变电压,I1、I2分别为原线圈和副线圈中的电流.下列说法正确的是( )
如图所示,电路中的变压器为理想变压器,S为单刀双掷开关.P是滑动变阻器R的滑动触头,U1为加在原线圈两端的交变电压,I1、I2分别为原线圈和副线圈中的电流.下列说法正确的是( )| A. | 保持P的位置及U1不变,S由a切换到b,则I1减小 | |
| B. | 保持P的位置及U1不变,S由b切换到a,则R上消耗的功率减小 | |
| C. | 保持U1不变,S由b切换到a,将P向上滑动,则I1增大 | |
| D. | 保持U1不变,S由a切换到b,将P向下滑动,则R上消耗的功率增大 |
| A. | 在最高点速度为零,加速度也为零 | |
| B. | 上升和下落过程的位移大小相同 | |
| C. | 从上升到下降的整个过程中加速度保持不变 | |
| D. | 上升到某一高度时的速率与下降到此高度时的速率相等 |